ФИЗИКА

2.4.2. Уравнение Ван-дер-Ваальса. Изотермы реальных газов. Фазовые переходы

Итак, для описания поведения реальных газов необходимо учитывать размеры молекул и их взаимодействие друг с другом. Было предложено много различных уравнений. Самым простым из них и вместе с тем дающим достаточно хорошие результаты оказалось уравнение, предложенное Ван-дер-Ваальсом. Это уравнение было получено путём внесения поправок в уравнение (2.2.19) и имеет вид

(2.4.2)

.

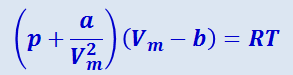Здесь р – давление, оказываемое на газ извне (равное давлению газа на стенки сосуда), α и b – постоянные Ван-дер-Ваальса, имеющие для разных газов различные значения, определяемые экспериментально. Единица измерения постоянной α - Па ⋅ м6/моль2, постоянной b - м3/моль .

Поправка α/V2m характеризует добавку к внешнему давлению, обусловленную взаимодействием между молекулами. Из-за притяжения молекул друг к другу газ как бы сжимает себя сам. Если бы взаимодействие между молекулами вдруг прекратилось, то для того, чтобы удержать газ в пределах того же объёма, понадобилось бы увеличить давление на величину, равную α/V2m. Обратная пропорциональность поправки квадрату объёма является следствием быстрого убывания сил притяжения между молекулами с увеличением расстояния r между ними.

Поправка к объёму «b» характеризует ту часть объёма сосуда, которая недоступна для движения молекул. Как показывает оценочный расчёт, «b» равно учетверённому суммарному объёму молекул газа.

От уравнения (2.4.2), написанного для одного моля газа, можно легко перейти к уравнению для произвольной массы газа т. Для этого нужно учесть, что 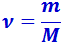молей газа занимают при тех же условиях объём V в ν раз бóльший, чем объём моля: V = νVm. Заменив в (4.2) Vm через V/ν, получим:

(2.4.3)

.

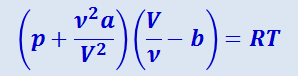Умножим обе части этого равенства на ν и введём обозначения:

(4.4)

.

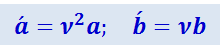Подставив (2.4.4) в (2.4.3) придём к уравнению Ван-дер-Ваальса для ν молей газа:

(2.4.5)

.

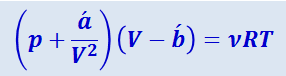С увеличением V роль поправок в уравнении (2.4.2) становится всё менее существенной, и в пределе это уравнение переходит в уравнение (2.2.19). Это согласуется с тем фактом, что реальные газы при уменьшении плотности приближаются по своим свойствам к идеальному газу.

Реальные газы следуют уравнению Ван-дер-Ваальса лишь приближённо.

Томас Эндрюс экспериментально исследовал зависимость молярного объёма углекислого газа от давления при изотермическом сжатии. Результаты этих опытов представлены на рис. 2,4.2 (T1<T<T2<Tкр.<T3<T4). При температурах T, меньших Tкр. = 340 K, на каждой изотерме имеется горизонтальный участок ВС, вдоль которого постоянна не только температура, но и давление p = pB, а молярный объём может принимать любые значения от VB до VC. Разность VC - VB объёмов в конечных точках горизонтальных участков изотерм возрастает с понижением температуры Т. Из рис. 2,4.2 видно, что эта разность объёмов стремится к нулю при приближении к температуре Tкр., которую называют критической температурой.

На изотерме, соответствующей температуре T = Tкр. (её называют критической изотермой), точки В и С сливаются в одну точку К, называемую критической точкой. Соответствующие ей значения давления pкр. и молярного объёма Vкр. называют критическими. Критическая точка совпадает с точкой перегиба изотермы T = Tкр., причём касательная к изотерме в этой точке параллельна оси Vm.

Любую докритическую изотерму (T < Tкр.) можно разбить на три характерных участка: ТС, СВ и ВА. Вдоль первого и третьего участков давление монотонно возрастает при уменьшении молярного объёма. На участке СВ сжатие углекислоты не сопровождается изменением её давления. Это своеобразие докритических изотерм связано с тем, что они охватывают различные агрегатные состояния CO2. Опыты показали, что на участке ТС углекислота находится в газообразном состоянии, а на участке изотермы ВА – в жидком. Малая сжимаемость жидкостей приводит к тому, что участок изотермы ВА представляет собой почти вертикальную прямую.

На участке СВ углекислота одновременно находится в двух агрегатных состояниях: жидком и газообразном. Точка С соответствует началу конденсации CO2 при изотермическом сжатии, а точка В – концу конденсации. Наоборот при изотермическом расширении жидкой углекислоты точка В соответствует началу кипения, а точка С – его концу. Следовательно, точка В соответствует состоянию кипящей жидкости, а точка С – состоянию сухого насыщенного пара.

В произвольном состоянии М области ВС CO2 представляет собой смесь кипящей жидкости и сухого насыщенного пара. Такую смесь называют влажным паром.

Для анализа состояния неоднородных систем, подобных влажному пару, в термодинамике вводится понятие фазы.

Фазой называют совокупность всех частей системы, обладающих одинаковым химическим составом, находящихся в одинаковом состоянии и ограниченных поверхностями раздела.

Таким образом, влажный пар представляет собой двухфазную систему, одна фаза которой – кипящая жидкость, а другая – сухой насыщенный пар.

Если нанести на диаграмму p - Vm точки В и С при различных температурах Т, то получим две пограничные кривые ВК и СК, смыкающиеся в критической точке К (рис. 2.4.2). Пограничная кривая кипения ВК отделяет однофазную область I жидкого состояния вещества от двухфазной области II его влажного пара. Она является кривой начала фазового перехода из жидкого состояния в газообразное и конца обратного фазового перехода из газообразного состояния в жидкое. Пограничная кривая конденсации СК отделяет двухфазную область II от однофазной области III газообразного состояния вещества.

При давлениях бóльше критического отсутствует область двухфазного состояния. Вещество находится либо в жидком, либо в газообразном состоянии. Границей между ними служит критическая изотерма.

Следовательно, газ, температура которого выше критической, нельзя перевести в жидкое состояние путём изотермического сжатия. В своё время потерпели неудачу первые попытки сжижения некоторых газов, критические температуры которых очень низки: у гелия tкр. = -268°С, у водорода tкр. = -240°С, у неона tкр. = -228°С и др. Это произошло из-за того, что не были известны их критические температуры и их пытались сжижать, изотермически сжимая при t > tкр.

Критическая точка замечательна тем, что при приближении к ней стирается различие между жидким и газообразным состояниями вещества. В критическом состоянии обращаются в нуль разность молярных объёмов кипящей жидкости и сухого насыщенного пара, удельная теплота парообразования и поверхностное натяжение жидкости.

Впервые вывод о необходимости существования для каждого вещества такой температуры, при которой исчезает различие между жидкой и газообразной фазами, находящимися в равновесии, был сделан Менделеевым.

Уравнение Ван-дер-Ваальса качественно правильно описывает некоторые особенности процесса сжижения газов. Это уравнение можно записать в такой форме:

(2.4.6)

.

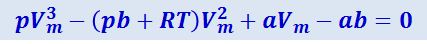Мы получили уравнение третьей степени относительно молярного объёма Vm. Коэффициенты уравнения зависят от давления, температуры и химической природы газа. В зависимости от числовых значений р и Т для данного газа это уравнение может иметь либо один, либо три действительных корня.

Изотермы газа, подчиняющегося уравнению (2.4.6), имеют вид, представленный на рис. 2.4.3, где T1<T2<T<T3<Tкр.<T6.

При температурах T < Tкр. имеется область состояний, где каждому значению давления соответствуют три точки изотермы, т.е. три различных изотермических состояния. По мере повышения температуры эти три точки сближаются и при T = Tкр. сливаются в одну точку К, которая является точкой перегиба изотермы T = Tкр.. Касательная к изотерме в точке К параллельна оси абсцисс. При температурах T >> Tкр. изотермы приближаются к равнобочным гиперболам – изотермам идеального газа.

Сравнение изотерм Ван-дер-Ваальса (рис. 2.4.3) с экспериментальными изотермами реальных веществ (например, с рис. 2.4.1) показывает, что изотермы Ван-дер-Ваальса охватывают не только область газообразного состояния вещества, но также области двухфазного и жидкого состояний. Жидкому состоянию соответствуют круто уходящие вверх левые участки изотерм. Однако в этой области имеется лишь качественное согласие с результатами экспериментов.

Волнообразные участки BDEFC изотерм Ван-дер-Ваальса (рис. 2.4.3), относящиеся к двухфазному состоянию вещества, сильно отличаются от соответствующих горизонтальных участков экспериментальных изотерм (штриховые прямые ВС). На основании второго закона термодинамики можно показать, что прямые рассекают участки изотерм BDEFC так, что площади BDEB и EFCE равны друг другу.

Опыты показывают, что некоторые состояния, соответствующие участкам BDEFC изотерм Ван-дер-Ваальса, практически осуществимы. Например, можно задержать кипение жидкости, тщательно удалив из неё механические примеси и производя нагревание в сосуде с гладкими стенками. При этом получают перегретую жидкость, различным состояниям которой соответствуют точки кривой BD. Аналогично при медленном изотермическом сжатии газа, не содержащего пылинок, ионов и других центров конденсации, можно получить пересыщенный пар, соответствующий участку изотермы CF. При введении в пересыщенный пар пылинок или ионов происходит быстрая конденсация пара. Это явление используют в камере Вильсона для наблюдения траекторий движения заряженных частиц. Участок изотермы DEF практически неосуществим.

Изотерма T = Tкр. является критической, а точка К перегиба этой изотермы – критической точкой. Значения критических параметров состояния pкр., Tкр. и молярного объёма Vкр. для газа, подчиняющегося уравнению Ван-дер-Ваальса, можно выразить через универсальную газовую постоянную и коэффициенты α и b:

(2.4.7)

.

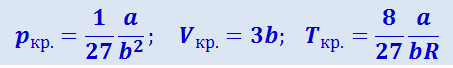Различают два типа превращений вещества из одной фазы в другую при изменении внешних условий: фазовые переходы первого ( I ) и второго ( II ) рода.

При фазовом переходе I рода скачкообразно изменяются такие характеристики вещества, как плотность, удельный и молярный объёмы, концентрации компонентов, и, что особенно характерно, выделяется или поглощается теплота, называемая теплотой фазового перехода. Примерами фазовых переходов I рода могут служить превращения вещества из одного агрегатного состояния в другое (испарение и конденсация, плавление и кристаллизация, сублимация и обратный ей процесс конденсации вещества из газовой фазы в твёрдую), фазовые превращения твёрдых тел из одной кристаллической модификации в другую, переход вещества из сверхпроводящего состояния в нормальное под действием сильного магнитного поля.

При фазовом переходе II рода теплота не выделяется и не поглощается (теплота фазового перехода II рода равна нулю), плотность изменяется непрерывно, а скачкообразно изменяются такие характеристики вещества, как молярная теплоёмкость, коэффициент теплового расширения, удельная электрическая проводимость, вязкость и др. Примерами фазовых переходов II рода могут служить: переход некоторых металлов и сплавов при низких температурах из нормального состояния в сверхпроводящее, переход жидкого гелия из одной модификации – He-I в другую – He-II, переход магнитного вещества из ферромагнитного состояния в парамагнитное и т.д.

к к к