ФИЗИКА

2.3.10. Неравенство Клаузиуса. Энтропия

Формулу к.п.д. идеальной тепловой машины, работающей по циклу Карно,

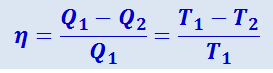
можно представить в несколько ином виде. Поделим левую часть на Q1, а правую – на T1. Тогда получим:

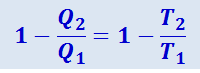
или

(2.3.43)

,

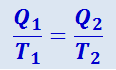где Q1 - подводимая теплота при температуре T1 при изотермическом расширении, а Q2 - выводимая теплота при температуре T2 при изотермическом сжатии.

Отношение количества переданной теплоты к температуре теплоотдатчика или теплоприёмника называется приведённой теплотой.

Соотношение (2.3.43) можно записать иначе, если вспомнить, что Q2 - величина отрицательная. С учётом этого будем иметь

(2.3.44)

,

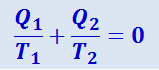т.е. для цикла Карно сумма приведённых теплот равна нулю.

До сих пор мы полагали, что теплоёмкость тел, обменивающихся теплом с рассматриваемой системой, велика настолько, что температура во время теплопередачи не меняется. Если это не так, то весь цикл можно разбить на бесконечное множество бесконечно узких циклов Карно и в течение одного элементарного процесса считать, что теплопередачи происходят при постоянных температурах Ti. Тогда получим:

,

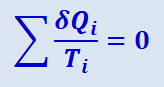а в пределе для любого обратимого цикла

(2.3.45)

.

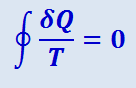Для реального (необратимого) цикла 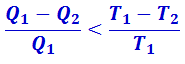, а значит

.

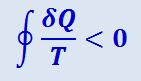В общем случае для любого цикла

(2.3.46)

.

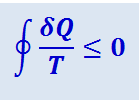Это неравенство Клаузиуса – общее математическое выражение второго начала термодинамики.

Из равенства нулю интеграла, взятого по замкнутому контуру (2.3.45), следует, что подинтегральное выражение 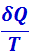есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние. Таким образом,

(2.3.47)

.

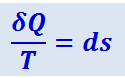Функция состояния, дифференциалом которой является 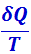, называется энтропией и обозначается s.

Из формулы (2.3.45) следует, что для обратимых процессов изменение энтропии равно

(2.3.48)

.

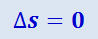В термодинамике доказывается, что энтропия системы, совершающей необратимый цикл, возрастает:

(2.3.49)

.

Выражения (2.3.48) и (2.3.49) относятся только к замкнутым системам, если же система обменивается теплотой с внешней средой, то её энтропия может вести себя любым образом.

Если система совершает равновесный переход из состояния 1 в состояние 2, то, согласно (2.3.47), изменение энтропии

(2.3.50)

,

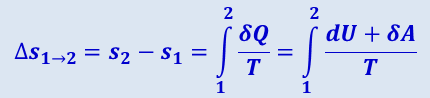где подинтегральное выражение и пределы интегрирования определяются через величины, характеризующие исследуемый процесс.

Формула (2.3.50) определяет энтропию лишь с точностью до аддитивной постоянной. Физический смысл имеет не сама энтропия, а разность энтропий.

Исходя из выражения (2.3.50), найдём изменение энтропии в процессах идеального газа. Так как

,

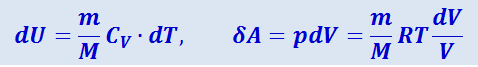то

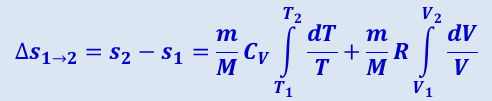
или

(2.3.51)

.

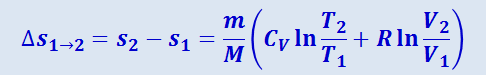Формула (2.3.51) выражает изменение энтропии при изобарном процессе. При изотермическом процессе (T1 = T2) она преобразуется к виду

;

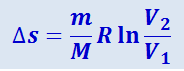при изохорном процессе (V1 = V2)

.

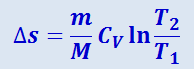Так как для адиабатического процесса δQ = 0, то Δs = 0 и, следовательно, s = const, т.е. адиабатический обратимый процесс протекает при постоянной энтропии.

Поэтому его часто называют изоэнтропийным процессом.

На часто используемой в термодинамике диаграмме Т, s цикл Карно выглядит предельно просто (рис. 2.3.13), причём не только для идеального газа, но и для веществ с какими угодно свойствами. На участке 1-2 рабочее тело получает от нагревателя с температурой T1 количество теплоты Q1, пропорциональное площади прямоугольника s1, 1, 2, s2. На участке 3-4 тело отдаёт холодильнику с температурой T2 количество теплоты Q2, пропорциональное площади прямоугольника s1, 3, 4, s2. Величина полученной телом теплоты пропорциональна площади прямоугольника 4, 1, 2, 3 цикла.

Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропий тел, входящих в систему.

Глубокий смысл энтропии вскрывается в статистической физике: энтропия связывается с термодинамической вероятностью состояния системы.

Как отмечено в п. 2.3.8, термодинамическая вероятность W состояния системы – это число способов (комбинаций), которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние (по определению W ≥ 1, т.е. термодинамическая вероятность не есть вероятность в математическом смысле (последняя ≤1)).

Больцман показал, что энтропия системы и термодинамическая вероятность связаны между собой следующим образом:

(2.3.51)

,

где k – постоянная Больцмана.

Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Формула (2.3.51) позволяет дать энтропии следующее статистическое толкование: энтропия является мерой неупорядоченности системы. В самом деле, чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия.

В состоянии равновесия – наиболее вероятного состояния системы – число микросостояний максимально, при этом максимальна и энтропия.

Так как реальные процессы необратимы, то можно утверждать, что все процессы в замкнутой системе ведут к увеличению её энтропии – принцип возрастания энтропии. При статистическом толковании энтропии это означает, что процессы в замкнутой системе идут в направлении увеличения числа микросостояний, иными словами, от менее вероятных состояний к более вероятным, до тех пор, пока вероятность состояния не станет максимальной.

Сопоставляя выражения (2.3.48) и (2.3.49) и (2.3.51), видим, что энтропия и термодинамическая вероятность состояний замкнутой системы могут либо возрастать, либо оставаться постоянными.

Отметим, что все эти утверждения имеют место только для систем, состоящих из очень большого числа частиц, но могут нарушаться в системах с малым числом частиц. Для «малых» систем могут наблюдаться флуктуации, т.е. энтропия и термодинамическая вероятность состояний замкнутой системы на определённом отрезке времени могут убывать, а не возрастать, или оставаться постоянными.

Используя понятие энтропии и неравенство Клаузиуса, второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия при этом возрастает.

В середине XIX в. возникла проблема так называемой тепловой смерти Вселенной. Рассматривая Вселенную как замкнутую систему и применяя к ней второе начало термодинамики, Клаузиус свёл его содержание к утверждению, что энтропия Вселенной должна достигнуть своего максимума. Это означает, что со временем все формы движения должны перейти в тепловое. Переход же теплоты от горячих тел к холодным приведёт к тому, что температура всех тел во Вселенной сравняется, т.е. наступит полное тепловое равновесие, и все процессы во Вселенной прекратятся – наступит тепловая смерть Вселенной. Ошибочность вывода о тепловой смерти Вселенной заключается в том, что бессмысленно применять второе начало термодинамики к незамкнутым системам, а по современным представлениям Вселенная, вероятнее всего, незамкнута.

Первые два начала термодинамики дают недостаточно сведений о поведении термодинамических систем при нуле Кельвина. Они дополняются третьим началом термодинамики, или теоремой Нернста-Планка: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина:

(2.3.52)

.

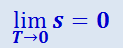к к к