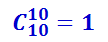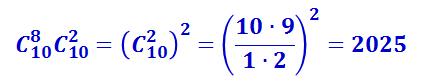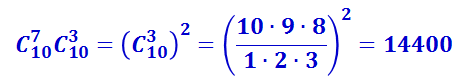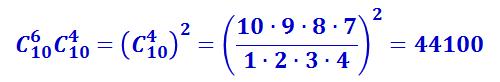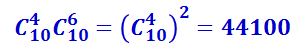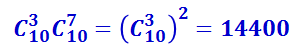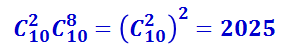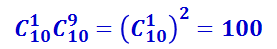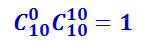ФИЗИКА

2.3.8. Обратимые и необратимые процессы

Обратимым называется процесс, который отвечает следующим условиям:

1) его одинаково легко можно провести в двух противоположных направлениях;

2) в каждом из этих случаев система проходит через одни и те же промежуточные состояния;

3) после проведения прямого и обратного процессов система и окружающие её тела возвращаются к исходному состоянию.

Всякий процесс, не удовлетворяющий хотя бы одному из этих условий, является необратимым.

Обратимыми являются процессы, протекающие в системах, где действуют консервативные силы.

Действительно, пусть абсолютно упругий шарик падает в вакууме на абсолютно упругую плиту. Пользуясь рассмотренными ранее законами упругого удара, нетрудно показать, что шарик, упав на плиту, вернётся после отражения в исходную точку, пройдя в обратном направлении все те промежутки состояния, которые он проходил при падении. После окончания процесса шарик и все окружающие его тела вернутся в первоначальное состояние, и это может повториться сколько угодно раз.

Нетрудно убедиться, что все квазистатические тепловые процессы также обратимы. Рассмотрим для примера квазистатический изотермический процесс.

Пусть газ квазистатически и вместе с тем изотермически расширился и его объём возрос на малую величину ΔV. Поскольку при данном процессе система всё время проходила через равновесные состояния, то очевидно, что в любой момент его можно направить в обратном направлении, т.е. сжать на ту же величину ΔV. При этом вся система пройдёт через те же промежуточные состояния, которые она проходила при расширении.

Газ при изотермическом расширении совершает работу, получая из окружающей среды путём теплообмена некоторое количество теплоты Q = A. Пусть эта работа пошла на увеличение потенциальной энергии какого-то тела массой т, которое поднимается на высоту h. Тогда из закона сохранения энергии следует, что Q = A = mgh. При обратном процессе тело опустится на ту же высоту h; потенциальная энергия груза пойдёт на совершение работы по сжатию газа: при этом газ отдаст окружающей среде путём теплообмена такое же количество теплоты, которое он получил при расширении.

Итак, после проведения процесса расширения, а затем сжатия газа он сам и все окружающие тела вернутся к начальным условиям, пройдя через одни и те же промежуточные состояния. Следовательно, квазистатический изотермический процесс обратим.

Аналогичные рассуждения позволят доказать обратимость и любых других квазистатических процессов.

Рассмотренные примеры обратимых процессов представляют собой идеализацию реальных природных явлений. На самом деле в природе нет строго консервативных систем; например, в любой реальной системе действуют силы трения. В природе нет также строго квазистатических процессов, ибо все тепловые процессы протекают не бесконечно медленно, а с конечной скоростью. А отсюда вытекает, что все реальные процессы в природе необратимы.

Не следует, однако, думать, что понятие об обратимом квазистатическом процессе является бессодержательным, а потому излишним. Аналогично таким идеализациям, как материальная точка, точечный заряд, консервативная система и т.п., понятие об обратимом процессе оказывается весьма удобной идеализацией реальных процессов, позволяющей в ряде случаев упростить решение той или иной конкретной задачи. Следует только всегда вначале проверить, в какой степени применение этой идеализации законно, в какой степени результаты идеализированного расчёта приближаются к результатам эксперимента.

Рассмотрим некоторые примеры, иллюстрирующие необратимость реальных тепловых процессов.

Как показывает опыт, при диффузии выравнивание концентраций происходит самопроизвольно, без внешнего воздействия. Обратный же процесс без внешнего воздействия никогда не пойдёт: сколько бы времени мы не ждали, не получится так, чтобы, например, смесь газов разделилась на исходные компоненты или растворённое в жидкости вещество (соль, сахар и т.п.) само по себе выделилось из этой жидкости.

Конечно, смесь можно разделить на исходные компоненты. Но при этом, во-первых, система не проходит через те промежуточные состояния, которые она проходила в процессе диффузии. А во-вторых, возвращение системы к исходному состоянию приводит к существенному изменению свойств окружающих её тел.

Так, разделяя газовую смесь, возникшую при диффузии, на исходные компоненты, мы должны затратить энергию на работу насосов; точно так же, выделяя, скажем соль из водного раствора путём дистилляции, мы расходуем энергию на испарение воды, что связано с изменением состояния окружающих данную систему тел.

Итак, диффузия является односторонним, а тем самым и необратимым процессом.

Опыт показывает, что теплообмен, как и диффузия, является односторонне направленным процессом. В результате теплообмена энергия передаётся сама собой всегда от тела с более высокой температурой к телу с более низкой температурой. Обратный процесс передачи энергии в форме тепла от холодных тел к горячим сам по себе никогда не происходит.

Одностороннее направление имеет также процесс превращения механической энергии во внутреннюю энергию при неупругом ударе или трении. Сколько бы мы ни ждали, не произойдёт обратный процесс самопроизвольного превращения внутренней энергии в механическую.

На первый взгляд необратимость тепловых процессов представляется парадоксальной. Действительно, все тепловые процессы в конечном счёте сводятся к механическим – к движению и взаимодействию молекул. Но ведь механические процессы обратимы; чем же вызвана необратимость тепловых явлений? Разрешить это кажущееся противоречие удаётся с помощью молекулярной статистики, в которой методы теории вероятностей применяются для изучения процессов, происходящих в системе, состоящей из огромного множества частиц. Суть её идей рассмотрим на простом примере модели сосуда с двумя сортами шаров.

Пусть на дне сосуда лежат два слоя шаров одинакового размера и одинаковой массы, но окрашенных в два цвета (рис. 3.3.11а). При встряхивании сосуда они перемешиваются (рис. 2.3.11б). Сколько бы мы потом не встряхивали сосуд, практически никогда не восстановится первоначальное состояние. Итак, процесс перемешивания шаров необратим – при встряхивании ящика упорядоченное расположение самопроизвольно переходит в беспорядочное, а обратный процесс сам по себе практически никогда не идёт. В чём же причина необратимости этого процесса? Откуда шары «знают», что нужно располагаться в беспорядке, а не упорядоченно? Ответить на этот вопрос можно будет, если мы сможем подсчитать, сколько всего имеется возможных комбинаций для распределения десяти чёрных и десяти белых шаров в два слоя.

Для облегчения расчёта обозначим все белые шары заглавными буквами алфавита, все чёрные – строчными:

Пусть в верхнем ряду лежат три белых шара и семь чёрных (рис. 2.3.11б). Естественно, что в нижнем ряду их число будет обратным – семь белых и три чёрных, так что выбор какого-либо распределения в верхнем ряду автоматически определяет их распределение в нижнем. Вычислим, сколько комбинаций шаров соответствует данному распределению. Из десяти белых шаров можно выбрать три шара разными способами: АВВ, АБЖ, ДЕК и т.д. Их число равно числу сочетаний, которые можно составить из десяти элементов по три. Оно обозначается 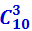и равно

.

Аналогично подсчитывается число способов, с помощью которых можно выбрать семь чёрных шаров из десяти:

.

Поскольку чёрные шары могут выбираться независимо от белых, то общее число комбинаций, с помощью которых можно осуществить распределение из трёх белых и семи чёрных шаров в верхнем ряду, равно произведению числа сочетаний из белых и из чёрных шаров, т.е. равно .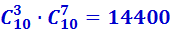

Аналогично можно подсчитать число комбинаций, соответствующих расположению из двух белых и восьми чёрных шаров, из четырёх белых и шести чёрных и т.д. Результаты подсчёта представлены в таблице 2.3.2.

Таблица 2.3.2

Будем встряхивать сосуд и каждый раз при этом фотографировать возникшее распределение шаров. Если сделать большое число снимков, например миллион, то из них примерно 5-6 снимков будут соответствовать распределению, когда внизу лежат все белые, а сверху – все чёрные шары; столько же снимков дадут обратную картину; число же снимков, соответствующих распределению, когда в каждом ряду находится пять белых и пять чёрных шаров, будет равно примерно 344000!

Итак, система из десяти белых и десяти чёрных шаров может находиться в одиннадцати различных состояниях. Однако каждое из этих состояний может быть реализовано разным числом комбинаций шаров.

Термодинамической вероятностью данного состояния некоторой системы тел называется число комбинаций отдельных элементов системы, с помощью которых реализуется это состояние.

Из таблицы 2.3.2 видно, что наибольшая термодинамическая вероятность соответствует равномерному распределению чёрных и белых шаров в обоих рядах (состояние №6) и состояниям №5 и №7, близким к равномерному. Наименьшая же термодинамическая вероятность соответствует полностью упорядоченному расположению шаров (состояния №1 и №11), а также состояниям №2 и №10, близким к полной упорядоченности.

Можно показать, что время пребывания некоторой системы в том или ином состоянии пропорционально термодинамической вероятности этого состояния. Тем самым становится ясной причина необратимости процесса перемешивания шаров. При встряхивании сосуда шары располагаются случайным образом, и в принципе может возникнуть любая комбинация. Однако чаще всего реализуется то состояние, термодинамическая вероятность которого больше.

Таким образом, необратимость процесса перемешивания шаров определяется термодинамической вероятностью тех состояний, в которых может пребывать данная система. Самопроизвольно идёт процесс перехода из состояния с малой термодинамической вероятностью в более вероятное состояние.

Обратный же процесс перехода из беспорядочного распределения шаров в упорядоченное состояние практически никогда сам по себе не происходит именно потому, что вероятность такого процесса ничтожна.

Аналогичный результат мы получим при анализе явлений в системе, состоящей из множества молекул, движущихся беспорядочно.

Очевидно, что явление диффузии во многом аналогично процессу перемешивания шаров. Поэтому для объяснения причины необратимости этого явления можно воспользоваться тем же методом.

Представим себе сосуд, разделённый пополам непроницаемой перегородкой; обе половины сосуда заполнены одинаковым числом молекул разных газов, например, водорода и кислорода. Если убрать перегородку, то в результате диффузии самопроизвольно возникнет однородная смесь газов. Однако сколько бы мы не ждали, смесь не разделится самопроизвольно на исходные компоненты.

Сравним вероятность «молекулярного беспорядка», соответствующего однородной смеси газов, с вероятностью «молекулярного беспорядка», соответствующего исходному распределению обоих газов по разным половинам сосуда.

Исходное распределение может быть реализовано только одним способом, следовательно, его термодинамическая вероятность равна единице. Однородную же смесь можно получить огромным числом способов: оно равно произведению числа сочетаний из N молекул водорода по N/2 молекул в каждой половине сосуда на такое же число сочетаний из N молекул кислорода по N/2 молекул в каждой половине. Итак, термодинамическая вероятность этого состояния

(2.3.35)

.

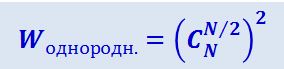В обычных условиях в одном кубическом миллиметре около 1016 молекул. При N = 1016 термодинамическая вероятность состояния, соответствующего однородной смеси газов, выражается огромным числом:

.

Отсюда ясна причина необратимости явления диффузии. Термодинамическая вероятность состояния однородной смеси несоизмеримо больше вероятности состояния, при котором оба компонента смеси разделены. А поэтому система самопроизвольно, за счёт беспорядочного движения молекул, переходит в наиболее вероятное состояние, соответствующее однородной смеси газов. Обратный же процесс разделения смеси на исходные компоненты настолько маловероятен, что практически никогда не происходит.

Понятие термодинамической вероятности может быть применено и для объяснения причины необратимости процесса превращения механической энергии во внутреннюю энергию при неупругом ударе. Однако, в отличие от случая диффузии, здесь подсчитать термодинамическую вероятность очень трудно.

Термодинамическая вероятность служит характеристикой направленности тепловых процессов. Сравнив вероятности двух состояний термодинамической системы, мы сразу установим направление процесса, который возможен в данной системе: это будет переход из менее вероятного в более вероятное состояние. Однако, как уже отмечено, вычисление термодинамической вероятности является весьма сложной задачей, так как практически чрезвычайно трудно подсчитать число различных комбинаций молекул, соответствующих тому или иному состоянию системы. Поэтому для термодинамических расчётов используется иная физическая величина – энтропия.

Энтропия, как и термодинамическая вероятность, - это физическая величина, характеризующая направленность процессов в природе.

к к к