ФИЗИКА
2.3.6. Применение первого начала термодинамики к изопроцессам
Среди равновесных процессов выделяются изопроцессы, при которых один из основных параметров состояния сохраняется постоянным.
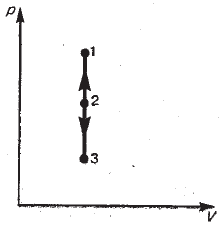
Изохорный процесс (V = const). Диаграмма этого процесса (изохора) в координатах p,V изображается прямой, параллельной оси ординат (рис. 2.3.6), где процесс 1-2 есть изохорное нагревание, а 2-3 – изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т.е.
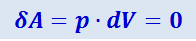 .
.
Из первого начала термодинамики (δQ = dU + δA) для изохорного процесса следует, что вся теплота, сообщаемая газу, идёт на увеличение его внутренней энергии:
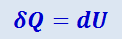 .
.
Согласно (2.3.11),
 .
.
Тогда для произвольной массы газа получим:
(2.3.17)
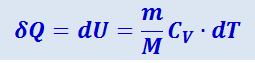 .
.
Рис. 2.3.6 |
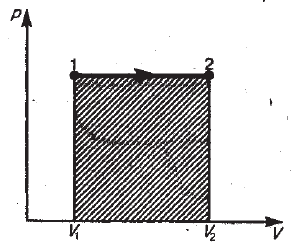
Изобарный процесс (p = const). Диаграмма этого процесса (изобара) в координатах p, V изображается прямой, параллельной оси V. При изобарном процессе работа газа (2.3.7) при увеличении объёма от V1 до V2 равна
(2.3.18)
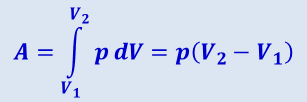
и определяется площадью заштрихованного прямоугольника (рис. 2.3.7). Если использовать уравнение Клайперона-Менделеева для выбранных нами двух состояний, то
 ,
,
откуда
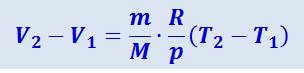 .
.
Рис.2.3.7 |
Тогда выражение (2.3.18) для работы изобарного расширения примет вид
(2.3.19)
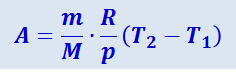 .
.
Из этого выражения следует физический смысл малярной газовой постоянной R: если T2 - T1 = 1 K, то для 1 моль R = A, т.е. R численно равна работе изобарного расширения 1 моль идеального газа при нагревании его на 1 К.
В изобарном процессе при сообщении газу массой т количества теплоты
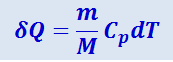
его внутренняя энергия возрастает на величину
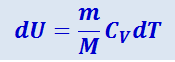 .
.
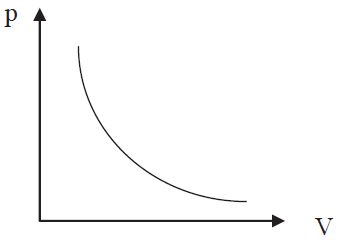
Изотермический процесс (Т = const). Он описывается законом Бойля-Мариотта pV = const. Диаграмма этого процесса (изотерма) в координатах p,V представляет собой гиперболу (рис. 2.3.8).
Рис. 2.3.8 |
Исходя из выражений (2.3.7) и уравнения Клайперона-Менделеева, найдём работу изотермического расширения газа:
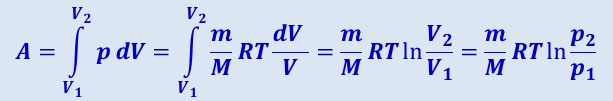 .
.
Так как при T = const внутренняя энергия идеального газа не изменяется:
 ,
,
то из первого начала термодинамики следует, что
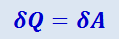 ,
,
т.е. всё количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:
(2.3.20)
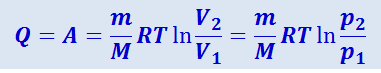 .
.
Следовательно, для того чтобы при расширении газа температура не понижалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное работе расширения.
Адиабатический процесс. Политропный процесс. Процесс, протекающий без теплообмена с внешней средой, называется адиабатическим. Чтобы найти уравнение адиабаты идеального газа, т.е. уравнение, связывающее параметры состояния идеального газа при адиабатическом процессе, воспользуемся уравнением (2.3.5) первого начала термодинамики, подставив в него выражения (2.3.17) и (2.3.6):
(2.3.21)
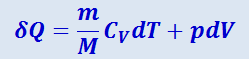 .
.
В отсутствие теплообмена с внешней средой δQ = 0. Поэтому для адиабатического процесса (3.21) преобразуется к виду
(2.3.22)
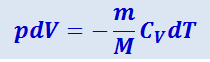 .
.
Продифференцировав уравнение состояния идеального газа 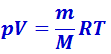 , получим:
, получим:
(2.3.23)
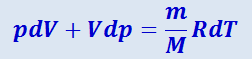 .
.
Исключив из (2.3.22) и (2.3.23) температуру Т, будем иметь:
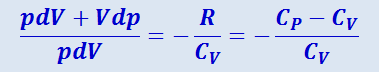 .
.
Разделив переменные и учитывая, что Cp/CV = γ, найдём:
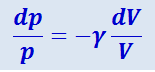 .
.
Интегрируя это уравнение в пределах от p1 до p2 и соответственно от V1 до V2, а затем, потенцируя, придём к выражению
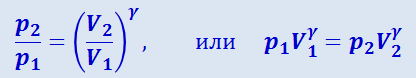 .
.
Так как состояния 1 и 2 выбраны произвольно, то можно записать
(2.3.24)
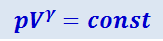 .
.
Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.
Для перехода к переменным T, V или р, Т исключим из (2.3.24) с помощью уравнения Клайперона-Менделеева
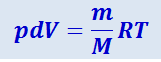
соответственно давление или объём:
(2.3.25)
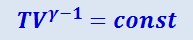 ;
;
(2.3.26)
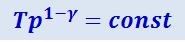 .
.
Из уравнения (2.3.25) вытекает, что при адиабатическом расширении идеальный газ охлаждается, а при сжатии нагревается.
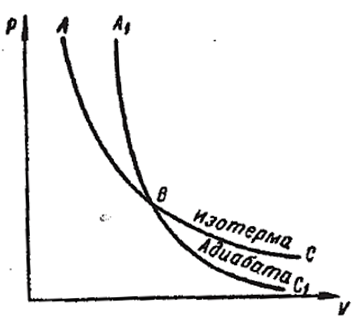
Рис. 2.3.9 |
Диаграмма адиабатического процесса (адиабата) в координатах p,V изображается гиперболой (рис. 2.3.9). Вычислим производную dp/dV для изотермы и адиабаты в одной и той же точке (p, V). Продифференцировав уравнение изотермы pV = const, получим, что pdV + V - dp = 0, откуда
(2.3.27)
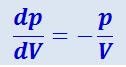 .
.
Дифференцирование уравнения адиабаты (2.3.24) даёт, что pγ ⋅ Vγ-1 dU + dVγ dp = 0, откуда
(2.3.28)
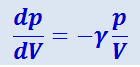 .
.
Из сравнения (2.3.28) и (2.3.27) следует: тангенс угла наклона касательной у адиабаты в γ раз больше, чем у изотермы – адиабата идёт круче, чем изотерма.
Вычислим работу, совершаемую газом в адиабатическом процессе. Запишем уравнение первого начала для адиабатического процесса δA = -dU в виде
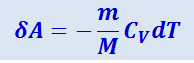 .
.
Если газ адиабатически расширяется от объёма V1 до V2, то его температура уменьшается от T1 до T2 и работа расширения идеального газа
(2.3.29)
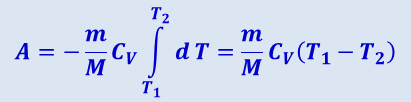 .
.
Применяя те же приёмы, что и при выводе формулы (2.3.24), выражение (2.3.28) можно преобразовать к виду
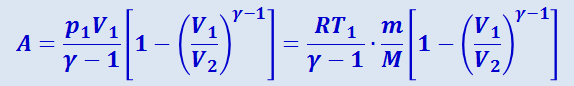 .
.
При выводе формул подразумевалось, что рассматриваемые процессы являются обратимыми. Мы знаем, что обратимыми могут быть только процессы, протекающие бесконечно медленно. Однако осуществить бесконечно медленный адиабатический процесс невозможно.
Близкими к адиабатическому процессу могут быть только достаточно быстро протекающие процессы. Скорость процесса должна быть, с одной стороны, настолько большой, чтобы теплообменом с внешней средой можно было пренебречь, а с другой стороны, достаточно малой для того, чтобы процесс можно было считать практически обратимым. Такие условия выполняются, в частности, в пределах небольших объёмов газа, в котором распространяется звуковая волна. Поэтому поведение газа при прохождении звуковой волны в пределах каждого достаточно малого объёма хорошо описывается уравнением адиабаты.
Рассмотренные изохорный, изобарный, изотермический и адиабатический процессы имеют общую особенность – они происходят при постоянной теплоёмкости. В первых двух процессах теплоёмкости соответственно равны CV и Cp, в изотермическом процессе (dT = 0) теплоёмкость равна ±∞, в адиабатическом (δQ = 0) теплоёмкость равно нулю. Процесс, в котором теплоёмкость остаётся постоянной, называется политропным.
Исходя из первого начала термодинамики при условии постоянства теплоёмкости можно вывести уравнение политропы:
(2.3.30)
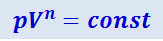 ,
,
где 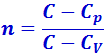 - показатель политропы. Очевидно, что при C = 0, n = γ, из (3.30) получается уравнение адиабаты;
- показатель политропы. Очевидно, что при C = 0, n = γ, из (3.30) получается уравнение адиабаты;
при C = ∞, n = 1 - уравнение изотермы;
при C = Cp, n = 0 - уравнение изобары;
при C = CV, n = ±∞ - уравнение изохоры.
Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.
к к к