ФИЗИКА

2.3.5. Теплоёмкость

Теплоёмкостью какого-либо тела называется величина, равная количеству тепла, которое нужно сообщить телу, чтобы повысить его температуру на один кельвин. Если сообщение телу количества тепла δQ повышает его температуру на dT, то теплоёмкость по определению равна

(2.3.8)

.

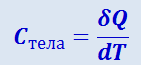Эта величина измеряется в джоулях на кельвин (Дж/К).

Теплоёмкость моля вещества, называемая молярной теплоёмкостью, обозначается прописной буквой С. Измеряется она в джоулях на моль-кельвин (Дж/моль⋅К).

Теплоёмкость единицы массы вещества называется удельной теплоёмкостью. Она обозначается строчной буквой с. Измеряется с в джоулях на килограмм-кельвин (Дж/кг⋅К).

Между молярной и удельной теплоёмкостями одного и того же вещества имеется соотношение

(2.3.9)

.

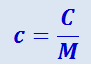Величина теплоёмкости зависит от условий, при которых происходит нагревание тела. Наибольший интерес представляет теплоёмкость для случаев, когда нагревание происходит при постоянном объёме или при постоянном давлении. В первом случае теплоёмкость называется теплоёмкостью при постоянном объёме (обозначается СV), во втором – теплоёмкостью при постоянном давлении (Cp).

Если нагревание одного моля происходит при постоянном объёме, то тело не совершает работы над внешними телами и, следовательно, согласно первому началу термодинамики (2.3.5), всё тепло идёт на приращение внутренней энергии моля

(2.3.10)

.

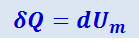Из (2.3.8) δQ = CV ⋅ dT, из (2.3.1) 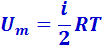. Подставив эти значения в (2.3.10), получим

(2.3.11)

.

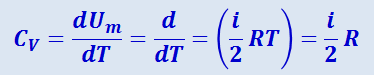Если нагревание одного моля происходит при постоянном давлении, то первое начало термодинамики можно записать в виде

(2.3.12)

,

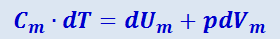где dVm - изменение объёма одного моля.

Из (2.3.12) следует:

(2.3.13)

.

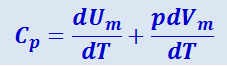Согласно (2.3.11), 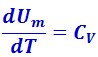, продифференцировав уравнение Клайперона-Менделеева pVm = RT по Т, получим pdVm = RdT. Подставив найденные значения в (2.3.13), будем иметь:

(2.3.14)

.

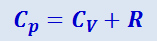Выражение (2.3.14) называется уравнением Майера; оно показывает, что Cp всегда больше CV на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении требуется ещё дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объёма газа. Использовав (2.3.11), выражение (2.3.14) можно записать в виде

(2.3.15)

.

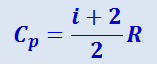При рассмотрении термодинамических процессов важно знать характерное для каждого газа отношение Cp к CV:

(2.3.16)

.

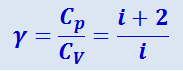Из формул (2.3.11) и (2.3.15) следует, что молярные теплоёмкости определяются лишь числом степеней свободы и не зависят от температуры. Это утверждение молекулярно-кинетической теории справедливо в довольно широком интервале температур лишь для одноатомных газов. Уже у двухатомных газов число степеней свободы, проявляющееся в теплоёмкости, зависит от температуры. Молекула двухатомного газа обладает тремя поступательными, двумя вращательными и одной колебательной степенями свободы.

По закону равномерного распределения энергии по степеням свободы для комнатных температур 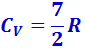. Из качественной экспериментальной зависимости молярной теплоёмкости водорода (рис. 2.3.5) следует, что CV зависит от температуры: при низкой температуре (≈ 50 К) 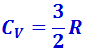, при комнатной - 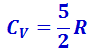(вместо расчётных 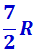) и при очень высокой - 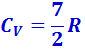. Это можно объяснить, предположив, что при низких температурах наблюдается только поступательное движение молекул, при комнатных – добавляется их вращение, а при высоких – к этим двум движениям добавляются ещё колебания молекул.

Расхождение теории и эксперимента нетрудно объяснить. Дело в том, что при вычислении теплоёмкости надо учитывать квантование энергии вращения и колебаний молекул (возможны не любые вращательные и колебательные энергии, а лишь определённый дискретный ряд значений энергий). Если энергия теплового движения недостаточна, например, для возбуждения колебаний, то эти колебания не вносят своего вклада в теплоёмкость (соответствующая степень свободы «замораживается» - к ней неприменим закон равнораспределения энергии). Этим объясняется, что теплоёмкость моля двухатомного газа – водорода – при комнатной температуре равна 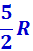вместо 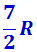. Аналогично можно объяснить уменьшение теплоёмкости при низкой температуре («замораживаются» вращательные степени свободы) и увеличение теплоёмкости при высокой температуре («возбуждаются» колебательные степени свободы).

к к к