ФИЗИКА

2.2.8. Явления переноса в газах

Беспорядочное движение молекул в газе ведёт к их непрерывному перемешиванию, отсюда два разнородных соприкасающихся газа взаимно проникают – диффундируют. Перенос молекул газа из одних мест в другие обуславливает также механизм явлений внутреннего трения в газах и теплопроводности. Все эти явления, связанные с движением молекул, носят название явлений переноса.

Во время развития кинетической теории газов против неё выдвигалось возражение: если скорости движения молекул действительно порядка нескольких сот метров в секунду, как этого требует кинетическая теория газов, тогда взаимное проникновение должно происходить весьма быстро. И если в какой-либо части комнаты открыть сосуд с пахучим веществом, то запах должен бы стать сразу заметным по всей комнате, так как молекулам вещества требуются лишь доли секунды, чтобы пролететь путь, равный размерам комнаты. На самом же деле известно, что диффузия газов при атмосферном давлении происходит медленно; в частности, медленно распространяются запахи. Ошибка в этих рассуждениях заключается в неучёте того, что молекулы, благодаря малой длине свободного пути при атмосферном давлении, непрерывно сталкиваются с другими молекулами, и, таким образом, «толкутся» на одном месте. Несмотря на большую скорость, молекула за одну секунду уходит лишь на очень небольшое расстояние от того места, где она находилась, путь её представляет весьма сложную и запутанную линию. Разберём, прежде всего, явление диффузии.

Диффузия. Наблюдения показывают, что при диффузии через некоторую площадку Δs переносится тем большая масса газа ΔM, чем больше размеры площадки Δs, чем бóльший промежуток времени Δt наблюдается диффузия и чем скорее меняется в направлении, перпендикулярном Δs, парциальная плотность ρ диффундирующего газа. Проведём ось ОХ нормально к площадке Δs. Пусть парциальная плотность рассматриваемого газа в двух точках, отстоящих друг от друга на отрезок ρx, отличается на Δρ, тогда величина 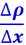характеризует изменение плотности газа ρ на единицу длины в направлении оси ОХ; эта величина называется градиентом плотности. По сказанному, ΔM пропорционально градиенту плотности , величине площадки Δs и времени Δt:

(2.2.47)

.

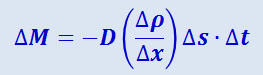Величина D, зависящая от сорта газа и от условий, при которых он находится, называется коэффициентом диффузии. Знак минус означает, что масса переносится в сторону убывания плотности.

Формула (2.2.47) характеризует явление диффузии с макроскопической точки зрения.

Рассмотрим теперь явление диффузии с точки зрения молекулярно-кинетической теории газов. Для простоты рассмотрим два различных, взаимно проникающих газа со столь сходными молекулами, что их массы и эффективные сечения можно считать равными друг другу. Такие молекулы будут иметь при одинаковых условиях одинаковые длины свободных путей и одинаковые скорости.

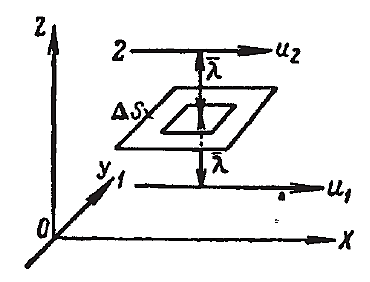
Подсчитаем число молекул одного из газов, пролетающих через площадку Δs (рис. 2.2.12), перпендикулярную оси ОХ, вдоль которой происходит изменение плотности газа ρ. Мысленно выделяем справа и слева от площадки на расстояниях от неё, равных среднему значению длины свободного пути 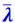, кубические объёмы А и В. Тогда можно считать, что молекулы, вылетающие из любого из этих кубиков, будут долетать без столкновений до площадки Δs.

Пусть боковые грани кубиков А и В будут параллельны площадке Δs и равны ей по величине; длину ребра кубиков обозначим через ℓ; очевидно, ℓ2 = Δs. Обозначим число молекул рассматриваемого газа, находящихся в кубике А через nA. Ввиду полной беспорядочности движения молекул, можно считать, что 1/3 этих молекул движется вдоль оси ОХ, из них половина – в направлении положительной оси ОХ и половина – в направлении отрицательной оси ОХ.

Таким образом, из числа молекул nA, находящихся в кубике А, число молекул, равное 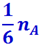, лежит по направлению к площадке Δs. Так как площадка Δs отстоит на 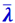от кубика, то все эти молекулы долетят до площадки Δs без столкновений и пролетят через неё. Время δt, в течение которого эти молекул пролетят через площадку Δs, равно тому промежутку времени, на который последние из молекул, вылетающие из кубика А в направлении площадки Δs, пролетят позже первых; отсюда 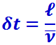, где - средняя арифметическая скорость молекул. Таким образом, число молекул ΔnA, пролетающих через площадку Δs за единицу времени слева направо, равно

.

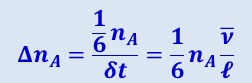Обозначим через n0 число молекул, приходящихся на единицу объёма в том месте, где находится кубик А, тогда nA = n'0ℓ2, и выражение для ΔnA можно написать в виде:

(2.2.48)

.

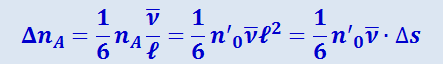Точно так же получим, что число молекул ΔnB, пролетающих через площадку Δs за единицу времени справа налево, будет

(2.49)

,

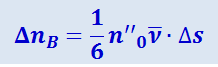где n''0 - число молекул в единице объёма в том месте, где находится кубик В.

Отсюда разность между числом молекул, пролетающих через площадку Δs слева направо и справа налево за некоторый промежуток времени Δt, равна

(2.2.50)

.

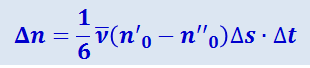Массу ΔM, переносимую через площадку Δs за время Δt слева направо (в направлении положительной оси ОХ), получим, умножив число перенесённых молекул Δn на массу одной молекулы т:

(2.2.51)

.

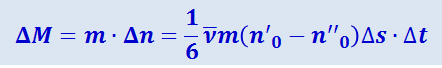Разность n'0 - n''0 равна скорости изменения числа молекул в единице объёма в направлении ОХ, т.е. величине , умноженной на расстояние между кубиками А и В; это расстояние равно 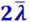, откуда

.

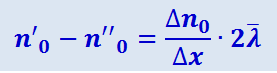Подставив это значение n''0 - n'0 в (2.2.51), получим:

;

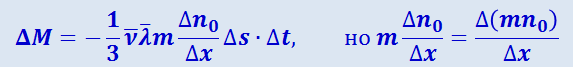величина mn0 равна массе рассматриваемого газа в единице объёма, т.е. равна плотности ρ, откуда

,

отсюда

(2.2.52)

.

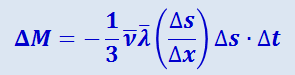Сопоставляя (2.2.52) и (2.2.48), получаем, что

(2.53)

.

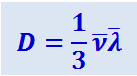Отметим, что в разреженных газах диффузия происходит быстрее, чем в газах при больших давлениях.

Внутреннее трение. При течении слоёв газа с разными скоростями между слоями возникают силы: более быстрый слой ускоряет соседний с ним более медленный слой и, наоборот, более медленный слой задерживает более быстрый. Возникающие при этом силы внутреннего трения f касательны к слоям газа.

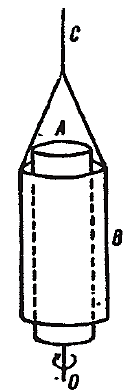
При обычных условиях внутреннее трение в газах гораздо меньше, чем в жидкостях, однако и оно может быть обнаружено на ряде опытов. Схема одного из таких опытов представлена на рис. 2.2.13. Пространство между двумя коаксиальными цилиндрами А и В заполнено испытуемым газом. Цилиндр А насажен на ось О и приводится в быстрое вращение; цилиндр В подвешен на нити С, угол закручивания которой может измеряться. При вращении цилиндра А он увлекает ближайшие к нему слои газа; последние, благодаря наличию внутреннего трения, увлекают за собой следующие слои и т.д. В результате вращающий момент оказывается приложенным к цилиндру В, который поворачивается, пока упругая сила закрученной нити С не уравновесит момент сил, приложенных к цилиндру В.

Если обозначить скорость течения слоёв газа через U, то силу внутреннего трения f можно выразить уравнением

(2.2.54)

,

где η - коэффициент внутреннего трения:

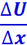- градиент скорости;

Δs - площадка, к которой приложена сила f.

Молекулярно-кинетическая теория объясняет это явление следующим образом. В текущем газе на скорость беспорядочного движения молекул ν наложена переносная скорость U, одинаковая для всех молекул данного слоя газа (текущего с определённой скоростью) и различная для различных слоёв (рис. 2.2.14). Молекулы, перелетая благодаря хаотическому движению из более быстрого слоя в более медленный, приносят с собой большую составляющую импульса mU и тем самым ускоряют более медленный слой. Наоборот, молекулы, попадающие из более медленного слоя в более быстрый, имеют слишком малую составляющую импульса, в результате чего они задерживают более быстрый слой.

Расчёт силы внутреннего трения f по этой модели приводит нас к уравнению

(2.2.55)

.

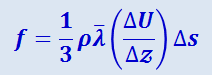Сравнивая выражения (2.2.55) и (2.2.54), видим, что они совпадают, если положить коэффициент внутреннего трения равным

(2.2.56)

.

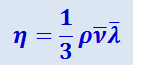Таким образом, молекулярно-кинетическая теория позволяет выразить коэффициент внутреннего трения через величины, характеризующие молекулярную структуру газа.

Формула (2.2.56) позволяет выяснить характер зависимости коэффициента внутреннего трения η от давления газа р. Из трёх величин 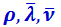, входящих в (2.2.56), скорость молекул не зависит от давления, из двух же остальных величин плотность ρ прямо пропорциональна давлению газа р, а средняя длина свободного пути молекул 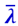обратно пропорциональна р. Следовательно, произведение 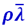не зависит от давления газа р, а значит, и коэффициент внутреннего трения η не зависит от давления газа р. Этот, на первый взгляд, парадоксальный результат обусловлен следующим: при понижении давления р уменьшается число частиц n0 в единице объёма, а следовательно, уменьшается и число частиц, переносящих импульс из одного слоя в другой. Но зато возрастает длина свободного пути молекул 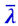, благодаря чему молекулы попадают в данный слой без столкновений из более далёкого слоя, движущегося с отличной скоростью U. В результате этих двух причин, действующих в противоположных направлениях, импульс, переносимый из слоя в слой, остаётся постоянным.

Теплопроводность. С макроскопической точки зрения явление теплопроводности заключается в переносе некоторого количества тепла ΔQ от более горячего слоя к более холодному. Если изменение температуры Т происходит в направлении оси ОХ, то через площадку Δs, перпендикулярную оси ОХ (рис. 2.2.15), за время Δt будет перенесено количество тепла ΔQ тем большее, чем больше площадка Δs, чем больше тот промежуток времени, за который наблюдается перенос тепла и чем быстрее происходит изменение температуры Т в направлении оси ОХ, т.е. чем больше градиент температуры 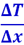. Суммируя, получим:

(2.2.57)

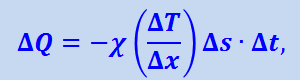
где χ – величина, зависящая от сорта газа и от условий, при которых он находится; эта величина называется коэффициентом теплопроводности.

Знак минус означает, что количество тепла ΔQ переносится в сторону убывания температуры Т.

С молекулярно-кинетической точки зрения процесс теплопроводности заключается в том, что молекулы из более горячего слоя, где они имеют бóльшую среднюю кинетическую энергию, проникая в более холодный слой, передают молекулам этого слоя часть своей энергии. Наоборот, молекулы из более холодного слоя, попадая в более горячий, получают от молекул более горячего слоя некоторое количество кинетической энергии. В результате более горячий слой охлаждается, а более холодный нагревается. Перенос количества тепла  ΔQ означает, с молекулярно-кинетической точки зрения, перенос через площадку Δs определённого количества кинетической энергии беспорядочного движения молекул.

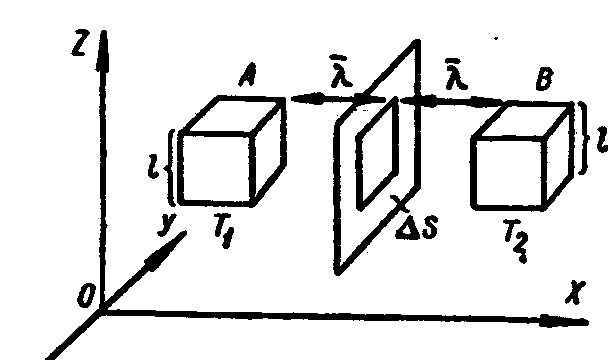
Введём в рассмотрение два кубика - А и В (рис. 2.2.15), расположенных от площадки Δs на расстояниях, равных средней длине свободного пути 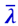, и подсчитаем количество тепла, переносимого через площадку Δs за время Δt.

Соответствующий расчёт приводит нас к уравнению

(2.2.58)

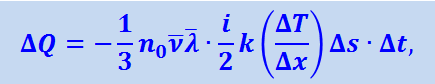
где i – число степеней свободы.

Сравнивая это выражение с (2.2.57), найдём, что коэффициент теплопроводности χ  равен:

(2.2.59)

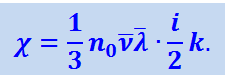
После очевидных преобразований (2.2.59) получим:

(2.2.60)

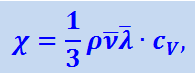
где CV - удельная теплоёмкость газа при постоянном объёме.

Коэффициент теплопроводности χ, как η, не зависит от давления газа. Это вытекает опять из того, что плотность ρ прямо пропорциональна, а средняя длина пути 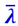обратно пропорциональна давлению р; скорость же молекул и удельная теплоёмкость CV от давления не зависят. Однако при очень низких давлениях коэффициент теплопроводности χ  начинает зависеть от давления.

Изложенные теории носят приближённый характер.

к к к