ФИЗИКА

2.2.7. Длина свободного пробега молекул

Молекулы, находясь в газе в состоянии непрерывного и хаотического движения, сталкиваются друг с другом; между столкновениями они проходят свободно некоторый путь λ. Длина этого пути между двумя столкновениями различна, но благодаря большому числу молекул и беспорядочности их движения можно говорить о средней длине свободного пути молекул .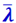

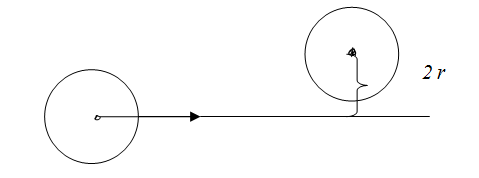
Рассмотрим некоторую определённую молекулу, которая движется со скоростью ν; молекулу представим себе в виде шарика радиусом r. После каждого столкновения молекула меняет направление скорости ν, однако для простоты предположим, что молекула продолжает после столкновения двигаться в том же направлении, в котором она двигалась до столкновения. Кроме того, для простоты положим, что все другие молекулы, кроме рассматриваемой, неподвижны. Тогда молекула заденет на своём пути все те молекулы, центры которых лежат на расстоянии не больше чем 2r (рис. 2.2.10) от прямой, вдоль которой она движется.

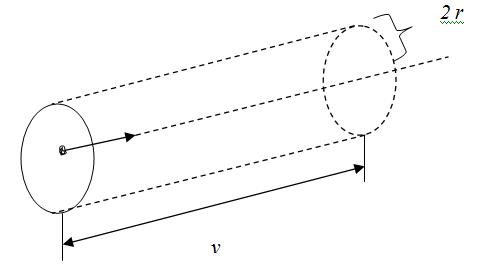
Следовательно, за единицу времени молекула заденет все те z молекул, центры которых лежат внутри цилиндра радиуса R = 2r и длины ℓ, численно равной скорости молекулы ν (рис. 2.2.11); число же молекул z, которые попадают внутрь такого цилиндра, равно

,

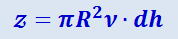где n0 - число молекул в единице объёма.

Подставляя сюда R = 2r и подразумевая под ν среднюю скорость движения молекул , получим выражение для среднего числа столкновений молекул в единицу времени:

(2.2.42)

.

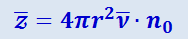Так как на самом деле другие молекулы тоже движутся, то для числа столкновений z получается несколько большее значение:

(2.2.43)

.

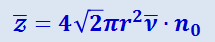Размеры молекул, как уже отмечалось, являются величинами порядка r ≅ 10-10 м; число молекул в единице объёма при нормальных условиях n0 ≅ 3 ⋅ 1025 м-3 и скорость молекул 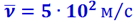. Подставив эти величины в (2.2.43), получим:

.

Таким образом, молекулы испытывают при нормальных условиях несколько миллиардов столкновений в секунду.

Среднюю длину свободного пути молекулы 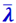получим, поделив средний путь, проходимый ею за единицу времени, на число столкновений в единицу времени . Так как путь, проходимый в единицу времени, численно равен скорости , то средняя длина свободного пути молекулы

(2.2.44)

.

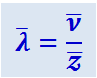Подставив (2.2.43) в (2.2.44), получим:

или, если ввести вместо радиуса молекулы её диаметр d, то

(2.2.45)

.

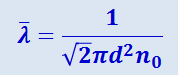Из (2.2.45) следует, что средняя длина свободного пути молекул обратно пропорциональна числу молекул в единице объёма n0. Так как при постоянной температуре n0 прямо пропорционально давлению газа, то получаем:

(2.2.46)

,

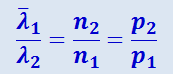где 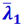и 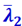- соответственно длины свободных путей молекул, относящиеся к давлениям газа p1 и p2.

Из (2.2.46) имеем: длина среднего свободного пути молекул 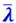обратно пропорциональна давлению газа р при постоянной температуре.

Существуют методы определения численного значения 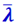для разных газов; по этим численным значениям 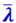по формуле (2.2.45) определяют диаметры молекул d. Надо иметь в виду, что найденные таким образом диаметры не представляют собой в точности действительных размеров молекул. Прежде всего, молекулы не являются правильными шарами; во-вторых, процесс столкновения молекул не похож на самом деле на соударение упругих шаров. Молекулы представляют собой сложные системы, состоящие из атомных ядер и электронов. Силы взаимодействия между ними, которые сказываются на малых расстояниях, носят сложный (отчасти электрический) характер. Процесс столкновения сводится к тому, что на малых расстояниях молекулы отталкиваются друг от друга, причём силы отталкивания возрастают по мере уменьшения расстояния между ними. В результате действия этих сил скорости молекул меняют своё направление.

Таким образом, диаметр молекул d, вычисленный в предположении, что молекулы являются упругими шариками, даёт лишь некоторое приближённое представление о размерах молекул; величина d является, как принято говорить, эффективным диаметром молекулы. Величина πr2 называется эффективным сечением молекулы.

Приближённый характер расчётов, приводящих к формуле (2.2.45), сказывается, в частности, в том, что средняя длина свободного пути молекул на самом деле несколько зависит от температуры. С повышением температуры она в некоторой степени повышается.

к к к