ФИЗИКА
2.2.5. Распределение молекул идеального газа по скоростям и энергиям теплового движения
Молекулы идеального газа в реальности движутся с различными скоростями. При этом при каждой температуре Т существует наиболее вероятная скорость νB. Молекулы, скорости которых много больше или много меньше наиболее вероятной, встречаются редко.
Ввиду полной беспорядочности движения молекул нельзя ставить вопроса о числе молекул, которые обладают точно заданной скоростью v, так как таких молекул в каждый данный момент вообще может не оказаться. Но можно поставить вопрос о числе молекул, скорости которых лежат в некотором определённом интервале скоростей, например, имеют значения, лежащие между некоторыми данными скоростями ν1 и ν2. Закон распределения скоростей был впервые получен Максвеллом.
При его выводе Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что силовые поля на газ не действуют.
Закон Максвелла описывается некоторой функцией f(ν), называемой функцией распределения молекул по скоростям. Поясним её смысл. Если разбить диапазон скоростей молекул на малые интервалы, равные dν, то на каждый интервал скорости будет приходиться некоторое число молекул dN(ν), имеющих скорость, заключённую в этом интервале. Если же удвоить число молекул N, то удвоится и число молекул dN(ν), скорости которых приходятся на данный интервал dν. Неизменной при этом останется величина
(2.2.27)
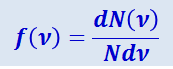 .
.
Таким образом, функция f(ν) определяет относительное число молекул dN(ν)/N, скорости которых лежат в диапазоне от ν до ν + dν, т.е. определяет характер распределения молекул по скоростям.
Вид этой функции был найден Максвеллом с помощью теории вероятностей:
(2.2.28)
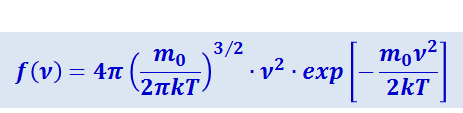 .
.
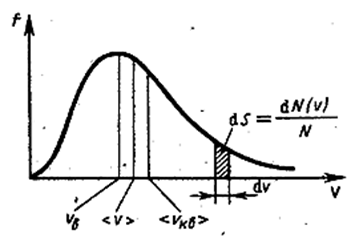
Из (2.2.28) следует, что конкретный вид функции зависит от рода газа (от массы молекулы и от параметра состояния (от температуры Т ). График функции (2.2.28) приведён на рис. 2.2.6. Так как при возрастании v множитель 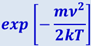 уменьшается быстрее, чем растёт множитель ν2, то функция f(ν), начинаясь от нуля, достигает максимума при νB и затем асимптотически стремится к нулю.
уменьшается быстрее, чем растёт множитель ν2, то функция f(ν), начинаясь от нуля, достигает максимума при νB и затем асимптотически стремится к нулю.
Рис. 2.2.6 |
Кривая несимметрична относительно νB. Относительное число молекул dN(ν)/N, скорости которых лежат в интервале от ν до ν + dν, находится как площадь заштрихованной полоски на рис. 2.2.6. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция f(ν) удовлетворяет условию нормировки
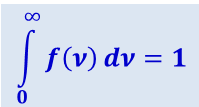 .
.
Скорость, при которой функция распределения молекул по скоростям максимальна, называется наиболее вероятной скоростью. Значение наиболее вероятной скорости можно найти, продифференцировав выражение (2.2.28) по аргументу ν, приравняв результат нулю и используя условие для максимума выражения f(ν):
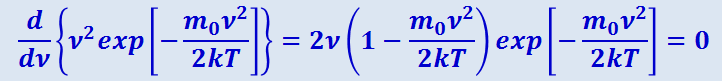
Значения ν = 0 и ν = ∞ соответствуют минимумам выражения (2.2.28), а значение ν, при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость νB:
(2.2.29)
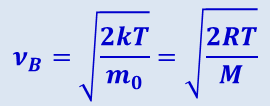 .
.
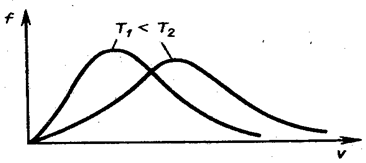
Из (2.2.29) следует, что при повышении температуры максимум функции распределения молекул по скоростям сместится вправо (рис. 2.2.7, значение вероятной скорости становится больше). Однако площадь, ограниченная кривой, остаётся неизменной, поэтому при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться.
Рис. 2.2.7 |
Для того, чтобы составить более конкретное представление о законе Максвелла, приведём следующие данные. Наиболее вероятная скорость молекул азота (М = 28) при 148°C равна
 .
.
При этом распределении молекул азота по скоростям будет следующее (табл. 2.1):
Таблица 2.2.1
Область скоростей, м/c |
Часть (%) общего числа молекул азота (Т = 421 К), имеющих скорости, заключённые в указанных пределах |
0 < v < 100 |
0,6 |
100 < v < 300 |
12 |
300 < v < 500 |
30 |
500 < v < 700 |
29 |
700 < v < 1000 |
23 |
1000 < v < |
5,4 |
Как видно, 59% от общего числа молекул имеют скорости, лежащие в области между 300 и 700 м/с, т.е. в области, на которую приходится и наиболее вероятная скорость νB = 500 м/с. Остальное число медленных молекул (ν < 100 м/с) и очень быстрых мало. Однако всё же число молекул, скорости которых более чем вдвое превышают наиболее вероятную (ν < 1000 м/с), достигает 5,4%. Наиболее вероятная скорость молекул данного газа определяется его температурой: она тем больше, чем выше температура; однако в газе и при невысоких температурах в некотором количестве присутствуют молекулы, движущиеся со значительными скоростями; наличие таких «горячих» молекул, как мы увидим в дальнейшем, играет весьма существенную роль для протекания многих процессов.
Кривая распределения скоростей Максвелла позволяет найти среднюю арифметическую скорость, для которой, как можно показать, получается значение
(2.2.30)
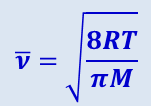 .
.
Таким образом, сопоставляя три рассмотренные нами скорости:
- наиболее вероятную
 ;
;
- среднюю арифметическую
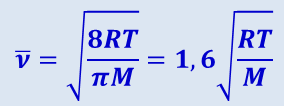 ;
;
- среднюю квадратичную
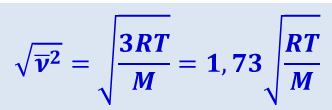 ,
,
видим, что наименьшей из них является наиболее вероятная, а наибольшей – средняя квадратичная (рис. 2.2.6). Отношение между этими скоростями не зависит ни от температуры, ни от рода газа.
Исходя из (2.2.28) можно найти распределение молекул газа по значениям энергии ε. Для этого перейдём от переменной ν к переменной 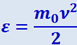 . Подставив в (2.2.28)
. Подставив в (2.2.28) 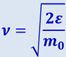 и
и  , получим:
, получим:
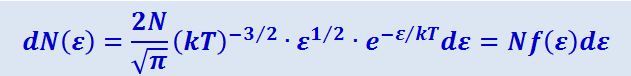 ,
,
где dNε - число молекул, имеющих кинетическую энергию поступательного движения, заключённую в интервале от ε до ε + dε.
Таким образом, функция распределения молекул по энергиям теплового движения имеет вид:
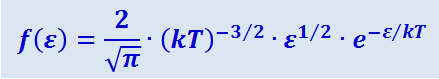 .
.
Средняя кинетическая энергия < ε > молекулы идеального газа
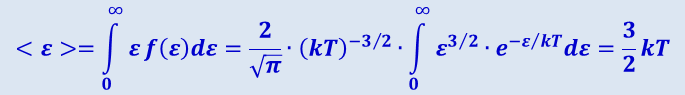 ,
,
что совпадает с формулой (2.2.13).
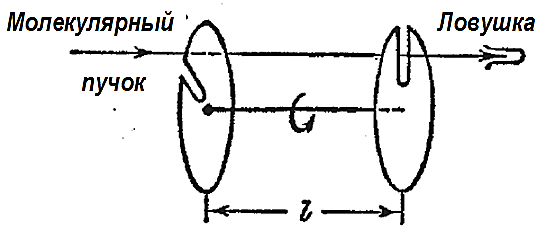
Распределение молекул по скоростям исследовалось экспериментально различными методами. Рассмотрим идею метода Ламмерта. Пучок молекул, выходящий из отверстия в сосуде, стенки которого поддерживались при заданной температуре, проходил через щель в первом диске (рис. 2.2.8). Через щель во втором диске могли пройти лишь те молекулы, которые долетали до него в тот момент, когда на их пути оказывалась щель в этом диске. Более медленные молекулы достигнут второго диска слишком поздно, а более быстрые – слишком рано для того, чтобы пройти через щель. Следовательно, такое устройство (называемое селектором скорости) выделяет из пучка молекулы, обладающие скоростями, заключёнными в узком интервале 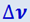 .
.
Рис. 2.2.8 |
Если диски вращаются с угловой скоростью ω, то они повернутся на угол φ между щелями за время t = φ/ω. За это время достигнут второго диска и, следовательно, пройдут через его щель молекулы, скорость которых 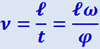 . Это и есть средняя скорость молекул, прошедших через селектор. Изменяя скорость вращения дисков, можно было выделить из пучка молекулы, обладающие скоростями в различных интервалах Δν. Улавливая эти молекулы в течение некоторого времени, можно было определить их количество.
. Это и есть средняя скорость молекул, прошедших через селектор. Изменяя скорость вращения дисков, можно было выделить из пучка молекулы, обладающие скоростями в различных интервалах Δν. Улавливая эти молекулы в течение некоторого времени, можно было определить их количество.
Результаты всех экспериментов, осуществлённых различными методами, оказались в полном согласии с распределением, полученным теоретически Максвеллом.
к к к