ФИЗИКА

8.4. Радиоактивные превращения ядер

Хорошо известно, что ряд атомных ядер из числа встречающихся в природе, например ядра радия Ra, урана U, тория Th и др., обладают способностью самопроизвольно испускать α-частицы, электроны и γ-кванты. Такие ядра (и элементы) называют радиоактивными. Про них говорят, что они обладают естественной радиоактивностью. Кроме того, к настоящему времени получено множество искусственно-радиоактивных ядер. Между искусственной и естественной радиоактивностью нет принципиального различия. Процесс радиоактивного превращения в обоих случаях подчиняется одинаковым законам.

Закон радиоактивного превращения. Отдельные радиоактивные ядра претерпевают превращения независимо друг от друга. Поэтому можно считать, что число ядер dN, распадающихся за малый промежуток dt, пропорционально как числу имеющихся ядер N, так и промежутку времени dt:

(8.4.1)

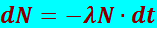
Здесь λ − характерная для данного радиоактивного вещества константа, называемая постоянной распада. Знак минус взят для того, чтобы dN можно было рассматривать как приращения числа нераспавшихся ядер N. Интегрируя (8.4.1), получим закон радиоактивного превращения

(8.4.2)

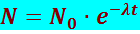
где N0 − количество ядер в начальный момент;

N − количество нераспавшихся ядер в момент времени t.

Количество ядер, распавшихся за время t, определяется выражением

(8.4.3)

Время, за которое распадается половина первоначального количества ядер, называется периодом полураспада Т. Это время определяется условием

,

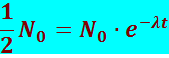откуда

(8.4.4)

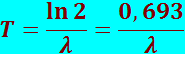
Период полураспада для известных в настоящее время радиоактивных ядер находится в пределах от 3⋅10-7 c до 5⋅1015 лет.

Определим среднее время жизни радиоактивного ядра. Количество ядер dN(t), испытывающих превращение за промежуток времени от t до t + dt, определяется модулем выражения (8.4.1). Время жизни каждого из этих ядер равно t. Следовательно, сумма времён жизни всех первоначально имевшихся ядер N0 равна интегралу t⋅dN(t).

Разделив эту сумму на N0, получим среднее время жизни радиоактивного ядра:

(8.4.5)

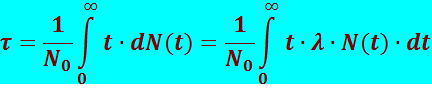
Подставив в (8.4.5) (8.4.2), будем иметь:

(8.4.6)

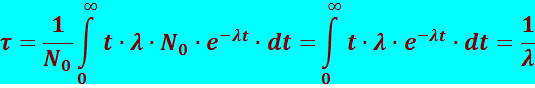
т.е. среднее время жизни есть величина, обратная постоянной распада.

Во всех видах радиоактивных превращений выполняются законы сохранения энергии, импульса, момента импульса, электрического, барионного и лептонного зарядов. При α-распаде и при γ-излучении выполняется закон сохранения чётности (при β-распаде он нарушается). Кроме того, при α-распаде выполняется закон сохранения изотопического спина (законы сохранения барионного и лептонного зарядов, чётности и изотопического спина будут рассмотрены ниже).

Активностью А нуклида (общее название атомных ядер, отличающихся числом протонов Z и нейтронов N) в радиоактивном источнике называется число распадов, происходящих с ядрами образца в 1 c:

(8.4.7)

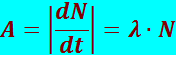
Единица активности в СИ – беккерель (Бк): 1 Бк – активность нуклида, при которой за 1 c происходит 1 акт распада. Внесистемной единицей активности является кюри (Ки): 1Ки = 3,7⋅1010 Бк.

Возникающие в результате радиоактивного распада ядра могут быть в свою очередь радиоактивными. Это приводит к возникновению цепочек или ряда радиоактивных превращений, заканчивающихся стабильным элементом. Совокупность элементов, образующих такую цепочку, называется радиоактивным семейством. Семейства называются по наиболее долгоживущему (с наибольшим периодом полураспада) «родоначальнику»: семейства тория , нептуния , урана и актиния . Конечными нуклидами соответственно являются , , , , т.е. единственное семейство нептуния (искусственно-радиоактивные ядра) заканчивается нуклидом Bi, а все остальные (естественно-радиоактивные ядра) нуклидами Pb.

α-распад. α-распад является свойством в основном тяжёлых ядер с массовыми числами А > 200 и зарядом Z > 82. Только небольшая группа α-активных ядер приходится на область с A = 140-160. При α-распаде из радиоактивного ядра испускается α-частица, т.е. ядро гелия 2He4, состоящее из двух протонов и двух нейтронов (дважды магическое ядро). Таким образом, дочернее ядро имеет на два протона и два нейтрона меньше, чем исходное. Примером может служить распад изотопа урана 92U238, протекающий с образованием 90Th234:

(8.4.8)

Возможность α-распада связана с тем, что масса (а значит и энергия покоя) α-радиоактивного ядра больше суммы масс (суммарной энергии покоя) α-частицы и образующегося после α-распада дочернего ядра. Избыток энергии исходного (материнского) ядра освобождается в форме кинетической энергии α-частицы и дочернего ядра.

Экспериментальными исследованиями установлено, что:

1) периоды полураспада естественно α-радиоактивных элементов, близко расположенных в периодической таблице Менделеева, различны и колеблются в пределах от 10-7 c до 1,4⋅1010 лет;

2) энергия вылетающих α-частиц мало отличаются друг от друга и составляют величину ~ 4 - 9МэВ;

3) существует связь между периодом полураспада и кинетической энергией α-частицы Е. Эта связь устанавливается эмпирическим законом Гейгера-Нэттола:

(8.4.9)

где А и В – некоторые эмпирические константы.

Из (8.4.9) следует: если энергия Е возрастает, то период полураспада уменьшается. При этом, если энергия меняется на 10%, то период полураспада меняется в 1000 раз.

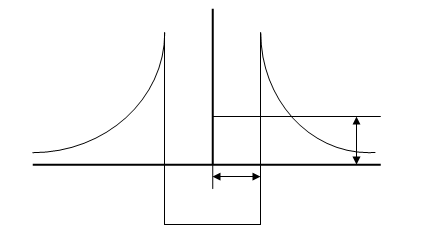
Классическая физика не может дать разумного объяснения α-распаду. Посмотрим, как объясняет это явление квантовая механика. Построим кривую зависимости потенциальной энергии от расстояния для системы: ядро тяжёлого элемента (например, урана) − α-частица. При её построении примем во внимание два обстоятельства:

1) на больших расстояниях от центра ядра, как это следует из опыта Резерфорда по рассеянию α-частиц, ядро отталкивает α-частицу по закону Кулона и потенциальная энергия системы будет описываться соотношением:

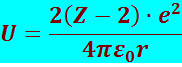
2) на малых расстояниях от центра ядра (r < R) преобладают ядерные силы. Эти силы весьма велики (как это отмечено выше), но имеют короткодействующий характер. Они создают потенциальную яму притяжения с очень крутыми краями (рис. 8.4.1).

Пусть в нашем ядре (внутри потенциальной ямы) содержится много протонов и нейтронов. Тогда группа из близко расположенных двух протонов и двух нейтронов случайно может оказаться вблизи границы, отделяющей область притяжения от области отталкивания, и может иметь импульс, направленный наружу, т.е. α-частица будет двигаться к «стенке» ядра. Поэтому задачу α-распада можно рассматривать в предположении, что в ядре существует α-частица, которая колеблется внутри потенциальной ямы в состоянии с энергией Е.

Допустимость такого приближения подтверждается тем, что α-частица имеет наибольшую энергию связи, что делает более вероятным испускание α-частицы (а не комбинации, например, одного нейтрона и одного протона). Энергия α-частицы внутри потенциальной ямы дискретна. Последнее подтверждается тем, что у одного и того же α-радиоактивного элемента имеется несколько групп α-частиц, отличающихся друг от друга энергиями.

Таким образом, задача сводится к определению поведения α-частиц внутри потенциальной ямы с дискретными уровнями энергии.

Если энергия α-частицы отрицательна, то ядро устойчиво по отношению к α-распаду, т.к. в этом случае для удаления α-частицы из ядра ей нужно сообщить энергию извне.

Если же энергия положительна, но всё же меньше, чем U(R) (рис. 8.4.1), то ядро находится в метастабильном состоянии. Для удаления частицы из ядра не требуется затраты энергии, но её испусканию мешает наличие потенциального барьера.

Опыты по рассеянию α-частиц тяжёлыми α-радиоактивными ядрами позволяют оценить величину этого барьера. В этих опытах α-частицы с энергией 8,8 МэВ до расстояний ~ 3⋅10-14 м рассеивались ядром 92U238 по закону Кулона, т.е. высота барьера для α-частицы больше, чем 8,8 МэВ, т.к. в противном случае α-частица проникла бы в ядро и была бы им захвачена (барьер ~ 30 МэВ).

Наряду с этим обнаружилось, что α-частицы, испускаемые ядром U238 имеют энергию лишь ~ 4 МэВ , т.е. много меньшую высоты барьера. Частица с такой энергией не может преодолеть барьер, но она может сквозь него туннелировать (за счёт экспоненциального «хвоста» волновой функции, описывающей движение α-частицы внутри потенциальной ямы).

Вероятностью ω туннельного эффекта для случая прямоугольного потенциального барьера шириной d описывается соотношением:

(8.4.10)

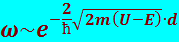
Из (8.4.8) видно, что вероятность увеличивается с уменьшением d и U - E, т.е. чем больше Е, тем больше вероятность вылета и тем меньше период полураспада. Полное квантовомеханическое решение этой задачи приводит к уравнению Гейгера-Нэттола и позволяет определить значения постоянных А и В, т.е. теория, основывающаяся на представлении о туннельном эффекте, приводит к результатам хорошо согласующимися с данными опыта.

β-Распад. Существуют три разновидности β-распада. В одном случае ядро, претерпевающее превращение, испускает электрон, в другом – его античастицу – позитрон, в третьем случае ядро поглощает один из электронов К-оболочки, значительно реже L- или М-оболочки (соответственно говорят о К-захвате, L-захвате или М-захвате).

Первый вид распада (β-− распад) протекает по схеме

(8.4.11)

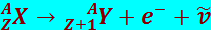
где Х и Y – символы элементов соответственно материнского и дочернего ядер;

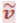− антинейтрино.

Чтобы подчеркнуть сохранение заряда и числа нуклонов в процессе β-распада, мы приписали β-электрону зарядовое число Z = -1 и A = 0.

Так как электроны не входят в состав ядер, то они должны как-то возникать в процессе их испускания; поскольку в этом случае отсутствует барьер, который мог бы задерживать электроны с энергией достаточной для вылета из ядра, то существование β--радиоактивных ядер с большими периодами полураспада можно объяснить только малой вероятностью процесса образования таких электронов.

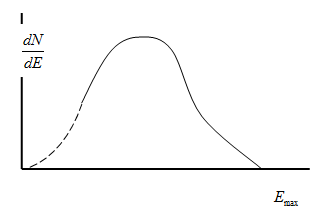
Экспериментальное изучение явления β--распада показало, что для всех β--радиоактивных элементов распределение вылетевших электронов по энергиям имеет вид, показанный на рис. 8.4.2. На нём площадь, охватываемая кривой, даёт общее число электронов, испускаемых в единицу времени, dN – число электронов, энергия которых заключена в интервале dE. Энергия Emax соответствует разности между массой материнского ядра и массами электрона и дочернего ядра. Следовательно, распады, при которых энергия электрона Е меньше Emax, протекают с кажущимся нарушением закона сохранения энергии.

Помимо кардинальной трудности с законом сохранения энергии, с β-распадом связана ещё одна трудность. Как известно, при β-распаде не изменяется число нуклонов в ядре. Поэтому не должен меняться и спин ядра, который равен целому числу ħ при чётном массовом числе А и полуцелому при нечётном.

Но вылет электрона, имеющего спин ħ/2, должен изменить спин ядра на величину ħ/2, т.е. ядро, имеющее, например, чётное число нуклонов должно было бы после β-распада иметь полуцелый спин и подчиняться другой квантовой статистике, продолжая сохранять в своём составе чётное число нуклонов, что противоречит экспериментальным и теоретическим данным о строении и свойствах атомных ядер.

Таким образом, явление β-радиоактивности поставило три трудные проблемы:

1. откуда берутся вылетающие электроны;
2. почему их энергии могут принимать всевозможные значения от нуля до Emax;
3. и как совместить сохранение при β-распаде спина ядра с тем, что электрон уносит из ядра спин, равный ħ/2.

Решение этих проблем было предложено Паули. Он предположил, что при β-распаде, помимо электрона, вылетает ещё одна частица, обладающая нулевым зарядом, ничтожно малой массой и спином равным ħ/2. Эта частица была названа Ферми нейтрино. Согласно современным представлениям частицей, испускаемой при β--распаде, является антинейтрино. Нейтрино выделяется при позитронном распаде.

Введение нейтрино и антинейтрино позволило сразу объяснить наличие сплошного энергетического спектра у β-радиоактивных излучателей. Полная энергия, теряемая ядром при испускании электрона, действительно равна Emax − энергии верхней границы β-спектра. Но она может различным образом распределиться между электроном и антинейтрино в соответствии с кривой β-спектра.

Легко в этом случае объясняется и сохранение спина ядра при β-распаде. Поскольку вместе с электроном уносится и антинейтрино, обладающее, как электрон, спином ħ/2, суммарный спин обеих частиц при взаимно противоположных спинах может быть равен нулю.

Рассмотрим вопрос о возникновении электронов при распаде. Как помним, при β--распаде число нуклонов в ядре не меняется, а заряд ядра увеличивается на единицу.

Очевидно, единственной возможностью осуществления этих условий является превращение в ядре нейтрона 0n1 в протон 1p1 с одновременным вылетом электрона и антинейтрино:

(8.4.12)

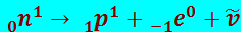
При этом превращении выполняются закон сохранения электрического заряда и законы сохранения импульса и момента импульса. Сохраняется также баланс массовых чисел.

Остаётся выяснить энергетическую возможность такого превращения. Оно должно сопровождаться выделением энергии, необходимой для образования электрона и антинейтрино при самопроизвольном протекании естественной β-радиоактивности. Превращение нейтрона в протон оказывается возможным ввиду различия масс и энергий покоя этих частиц.

Масса покоя нейтрона превышает массу атома водорода на 0,837⋅10-3 а.е.м. Этой массе соответствует энергия 782 КэВ. За счёт этой энергии может происходить самопроизвольное превращение нейтрона в протон. 782 КэВ должен при этом распределиться между электроном и антинейтрино.

Изложенная теория получила подтверждение в 1950 году, когда было экспериментально обнаружено, что свободные нейтроны действительно распадаются по схеме (8.4.12) с периодом полураспада 12,8 мин. Оказалось, что электроны, возникающие при распаде нейтрона, имеют непрерывный спектр, подобный изображённому на рис. 8.4.2. При этом Emax = 782 КэВ.

Примером β--распада может служить превращение 28Ni65 в 29Cu65:

Второй вид распада (β+-распад или позитронный распад) протекает по схеме:

(8.4.13)

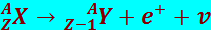
В качестве примера можно привести превращение 30Zn65 в 29Cu65:

Из схемы (8.4.13) видно, что атомный номер дочернего ядра на единицу меньше, чем материнский. Процесс сопровождается испусканием позитрона e+ и нейтрино ν.

β+-распад протекает так, как если бы один из протонов исходного ядра превратился в нейтрон, испустив при этом позитрон и нейтрино:

(8.4.14)

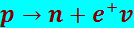
Для свободного протона такой процесс невозможен по энергетическим соображениям, так как масса протона меньше массы нейтрона. Однако протон в ядре может заимствовать требуемую энергию от других нуклонов, входящих в состав ядра.

Третий вид β-распада (электронный захват) заключается в том, что ядро поглощает один из К-электронов (реже из L- или М-электронов) своего атома, в результате чего один из протонов превращается в нейтрон, испуская при этом нейтрино:

(8.4.15)

Схема процесса выглядит следующим образом:

(8.4.16)

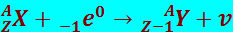
Место в электронной оболочке, освобождённое захваченным электроном, заполняется электронами из вышележащих слоёв, в результате чего возникают рентгеновские лучи, по которым и определяется сам захват. Примером электронного захвата может служить превращение 19K40 в 18Ar40:

(8.4.17)

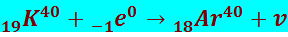
Окончательно существование нейтрино (антинейтрино) было доказано в опытах, выполненных в 1953–1954 гг.

Теория β-распада была построена в 1934 г. Она связывает между собой энергию β-распада и время жизни β-радиоактивного ядра. Согласно теории β-распад происходит под действием слабого взаимодействия, ответственного за медленные процессы.

β-радиоактивные ядра можно создать искусственно, если присоединить к стабильному ядру (или отнять у него) один или несколько однотипных нуклонов. Ядра с избытком нейтронов проявляют искусственную β--радиоактивность. Такие ядра получаются облучением веществ нейтронами в ядерных реакторах. Ядра с избытком протонов проявляют искусственную β+- радиоактивность или испытывают е-захват. Их можно получить, облучив вещества на циклотроне положительными ионами. Впервые искусственная β+- радиоактивность была открыта в 1934 г. при облучении веществ α-частицами, а искусственная β-- радиоактивность (в том же году) − при облучении веществ нейтронами от нейтронных источников.

Гамма-излучение. Гамма-излучение не является самостоятельным видом радиоактивности. Оно только сопровождает α- и β-распады, а также возникает в ряде других явлений.

В процессе α- и β-распадов дочернее ядро возникает чаще всего в возбуждённом состоянии. За время 10-13-10-14 cоно самопроизвольно переходит в основное состояние (ядра, подобно атомам, имеют дискретные уровни энергии). При этом избыток энергии ядра освобождается в виде кванта коротковолнового электромагнитного излучения − γ-кванта (подавляющая часть энергии) и в виде энергии отдачи ядра (ничтожно малая часть энергии). γ-излучение большинства ядер является столь коротковолновым, что его волновые свойства проявляются весьма слабо. Здесь на первый план выступают корпускулярные свойства, поэтому γ-излучение рассматривают как поток частиц γ-квантов. Энергия γ-квантов, испускаемых после α-распада, обычно не превышает 0,5 МэВ. Энергия γ-квантов, испускаемых после β-распада, достигает 2-2,5 МэВ.

В некоторых случаях энергия возбуждения ядра идёт не на γ-излучение, а передаётся одному из электронов данного атома, в результате чего электрон вылетает из него. Этот процесс называется внутренней конверсией, а вылетевший электрон – конверсионным. Конверсионные электроны в отличие от электронов β-распада имеют не непрерывный, а дискретный спектр. Внутренняя конверсия всегда сопровождается характеристическим рентгеновским излучением.

γ-кванты, обладая нулевой массой покоя, не могут замедляться в среде. Поэтому при прохождении γ-излучения сквозь вещество они либо поглощаются, либо рассеиваются им. Основными процессами, сопровождающими прохождение γ-излучения через вещество, являются фотоэффект, эффект Комптона и образование электронно-позитронных пар.

γ-излучение – самое проникающее излучение. Это свойство используется в гамма-дефектоскопии.

Воздействие γ-излучения (а также других видов ионизирующего излучения) на вещество характеризуют дозой ионизирующего излучения. Различаются:

1) Поглощённая доза излучения – физическая величина, равная отношению энергии к массе облучаемого вещества. Единица поглощённой дозы излучения – грей (Гр): 1 Гр = Дж/кг − доза излучения, при которой облучённому веществу массой 1 кГ передаётся энергия любого ионизирующего излучения 1 Дж.

2) Экспозиционная доза излучения – физическая величина, равная отношению суммы электрических зарядов всех ионов одного знака, созданных электронами, освобождёнными в облучённом воздухе (при условии полного использования ионизирующей способности электронов), к массе этого воздуха. Единица экспозиционной дозы излучения – кулон на килограмм (Кл/кГ); внесистемной единицей является рентген (Р): 1Р = 2,58⋅10-4 Кл/кГ.

3) Биологическая доза – величина, определяющая воздействие излучения на организм.

Единица биологической дозы – биологический эквивалент рентгена (бэр): 1 бэр – доза любого вида ионизирующего излучения, производящая такое же биологическое действие, как и доза рентгеновского или гамма-излучения в 1 Р (1 бэр = 10-2 Дж/кГ).

Мощность дозы излучения – величина, равная отношению дозы излучения к времени облучения. Различают:

1) мощность поглощённой дозы (единица – Гр/с);

2) мощность экспозиционной дозы (единица – ампер на килограмм, А/кГ).

Эффект Мёссбауэра. Атомы особенно интенсивно поглощают свет частоты, соответствующей переходу из основного в ближайшее к нему возбуждённое состояние. Это явление называется резонансным поглощением. Возвращаясь затем в основное состояние, атомы испускают фотоны резонансной частоты. Соответствующее излучение носит название резонансного излучения или резонансной флуоресценции. Явление резонансной флуоресценции было открыто Р. Вудом в 1904 г. Вуд обнаружил, что пары натрия при облучении их светом, соответствующим жёлтой линии натрия, начинают светиться, испуская излучение той же длины волны. Впоследствии аналогичное свечение наблюдалось во многих других случаях. Вследствие резонансного поглощения свет, прошедший через флуоресцирующее вещество, ослабляется.

Атомные ядра, как и атомы, имеют дискретные уровни энергии, и можно было ожидать, что для γ-лучей существует явление ядерной резонансной флуоресценции. Однако наблюдать резонансную флуоресценцию с γ-лучами долгое время не удавалось. Причина этого состоит в следующем. Как отмечено выше, при переходе ядра из возбуждённого состояния с энергией Е в основное (его энергия принята равной нулю) γ-квант имеет энергию Еγ  несколько меньшую, чем Е, из-за отдачи ядра в процессе излучения:

(8.4.18)

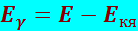
где Екя − кинетическая энергия отдачи ядра.

При возбуждении же ядра и переходе его из основного состояния в возбуждённое с энергией Е γ- квант должен иметь энергию

(8.4.19)

где Екя − энергия отдачи, которую γ-квант должен передать поглощающему ядру.

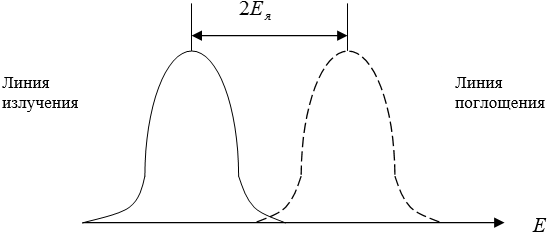
Таким образом, максимумы линий излучения и поглощения сдвинуты относительно друг друга на величину 2Ея (рис. 8.4.3). Используя закон сохранения импульса, согласно которому в рассмотренных процессах излучения и поглощения импульсы γ-кванта и ядра должны быть равны, получим

(8.4.20)

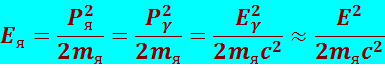
где mя − масса ядра.

Из вышесказанного следует, что резонансное поглощение γ-излучения в принципе может быть получено только при компенсации потери энергии на отдачу ядра. Эту задачу решил в 1958 году Мёссбауэр. Он исследовал излучение и поглощение γ-излучения ядрами иридия 77Ir191, находящимися в кристаллической решётке, т.е. в связанном состоянии (при этом источник излучения и поглотитель охлаждались жидким гелием).

В этих условиях импульсы и энергия отдачи передаются не одному ядру, излучающему (поглощающему) γ-квант, а всей кристаллической решётке в целом. Так как кристалл обладает гораздо большей массой по сравнению с массой отдельного ядра, то в соответствии с формулой (8.4.20) потери энергии на отдачу становятся исчезающее малыми, а значит процессы излучения и поглощения γ-излучения происходят практически без потерь энергии, т.е. идеально упруго.

Это явление упругого (т.е. не сопровождающегося изменением внутренней энергии тела) испускания или поглощения γ-квантов было названо эффектом Мёссбауэра. При рассмотренных условиях линии излучения и поглощения γ-квантов практически совпадают и имеют весьма малую ширину, равную естественной ширине Г. Естественная ширина Г определяется из соотношения неопределённостей:

(8.4.21)

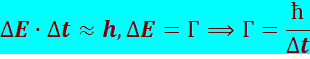
Для 77Ir191 время жизни возбуждённого состояния

.

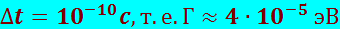Позже эффект Мёссбауэра был открыт в 26Fe57 и для ряда других веществ. Ядро Fe57 замечательно в том отношении, что для него эффект наблюдается при температуре до 1000°C, так что нет необходимости в охлаждении. Кроме того, 57Fe отличается чрезвычайно малой естественной шириной линии.

Мёссбауэр вооружил экспериментальную физику новым методом измерений невиданной прежде точности.

Кроме рассмотренных ранее радиоактивных процессов (α, β - распад и γ-излучение) известно ещё несколько процессов, происходящих по закону радиоактивного распада – это протонная радиоактивность, спонтанное деление тяжёлых ядер, испускание запаздывающих нейтронов, испускание запаздывающих протонов, запаздывающая двух протонная радиоактивность и запаздывающая двух нейтронная радиоактивность.

к к к