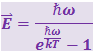К содержанию

Задача 7.1

Вблизи абсолютного нуля удельная теплоёмкость c0 = kT3, где k – постоянная, разная для разных материалов. Найти формулу, дающую количество тепла, необходимого для нагревания твёрдого тела массой т от Т1 до Т2.

Задача 7.2

Найти молярную теплоёмкость твёрдого тела, если среднее значение энергии, приходящейся на одну степень свободы, определяется формулой Планка .

Задача 7.3

Пользуясь законом Дюлонга и Пти, найти, из какого материала сделан металлический шарик массой 25 г, если известно, что для его нагревания от 10°С до 30°С потребовалось 28 кал.

Задача 7.4

В образце германия подвижность электронов равна Un = 0,36 м2/В×с, а дырок Up = 0,18 м2/В×с. В этом образце осуществляется собственная электропроводность. Какая часть тока переносится дырками?

Задача 7.5

Найти изменение электропроводности образца чистого германия при облучении его монохроматическим светом длиной волны 1,24 E, если величина поглощённой световой энергии равна E = 2,8 ⋅ 10-6Дж (Un = 0,36 м2/В×с, Up = 0,18 м2/В×с).

Задача 7.6

Красная граница фотоэффекта сурьмяно-цезиевого фотокатода соответствует длине волны λ1 = 6500 E (при очень низких температурах). Красная граница собственной фотопроводимости отвечает длине волны λ2 = 207⋅10-6 м. Определить в электрон-вольтах положение дна зоны проводимости относительно вакуума.

Задача 7.7

Кремниевый образец нагревают от температуры t1 = 0°C до t2 = 10°C. Во сколько раз возрастает его удельная проводимость (ширина запрещённой зоны Eф = 1,1 эВ).

Задача 7.8

Вычислить максимальную энергию (ЕФ), которую могут иметь свободные электроны в меди при 0 К. Принять, что на каждый атом приходится по одному электрону.

Задача 7.9

При каких условиях можно применять статистику Максвелла-Больцмана к электронам в металле? Получить распределение Максвелла-Больцмана из распределения Ферми-Дирака.