ФИЗИКА

7.28. Понятие о сверхпроводимости

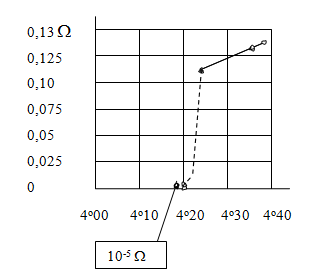
Явление сверхпроводимости. Пытаясь выяснить роль примесей в формировании остаточного сопротивления, Комерлинг-Оннес провёл в 1911 г. опыты с предельно очищенной ртутью. Результаты этих опытов оказались неожиданными: при температуре TK = 4,2 K электрическое сопротивление ртути ρ падало до нуля. На рис. 7.28.44 дан график зависимости электрического сопротивления ртути, взятый из статьи Оннеса, в которой было описано открытие сверхпроводимости. Значок Ω означает омы.

Температура Тк, при которой происходит переход в сверхпроводящее состояние, называется критической температурой перехода. Для таллия, олова и свинца она равна соответственно 2,35; 3,73 и 7,19 K. Самой высокой критической температурой среди чистых веществ обладает ниобий (TK = 9,22 K), а наиболее низкой – иридий (TK = 0,140 K).

Критическая температура зависит не только от химического состава вещества, но и от структуры самого кристалла. Известно, что кристаллы многих веществ могут существовать в различных модификациях. Эти модификации отличаются своими физическими свойствами. Так, например, существуют две различные модификации лантана (α - L0 и β - L0), причём каждая из них характеризуется своей критической температурой (для α - LaTK = 4,8 K, для β - LaTK = 5,95 K). В настоящее время насчитывается более 1000 сверхпроводящих материалов, причём основную их часть составляют не чистые вещества, а их сплавы и соединения. Из сказанного следует, что сверхпроводимость является свойством не отдельных атомов, а представляет собой коллективный эффект, связанный со структурой всего образца.

Так как, согласно закону Ома, , то требование ρ = 0 при конечной плотности тока, означает, что напряжённость электрического поля ε в любой точке сверхпроводника равна нулю: ε = 0.

Экспериментально сверхпроводимость можно наблюдать различными способами. Рассмотрим два из них:

1) включим в общую электрическую цепь, по которой течёт ток, звено из сверхпроводника. В момент перехода в сверхпроводящее состояние разность потенциалов на концах этого проводника обращается в нуль;

2) поместим кольцо из сверхпроводника в перпендикулярное к нему магнитное поле. Охлаждаем это кольцо до температуры ниже Тк и выключаем поле. В кольце при этом индуцируется незатухающий ток. Ток в кольце регистрируется магнитным полем, которое он создаёт.

Опыты, проведённые в Массачусетском технологическом институте, показали, что ток в несколько сотен ампер, наведённый в сверхпроводящем кольце, сохранялся неизменным в течение года.

Сверхпроводник в магнитном поле. Мейсснер и Оксенфельд установили, что за явлением сверхпроводимости скрывается нечто большее, чем идеальная сверхпроводимость, т.е. равенство нулю удельного сопротивления. Они обнаружили, что магнитное поле выталкивается из сверхпроводника независимо от того, чем это поле создано – внешним источником или током, текущим по самому сверхпроводнику. Это означает, что магнитная индукция Bi внутри сверхпроводника всегда равна нулю, пока он находится в сверхпроводящем состоянии; иначе говоря, сверхпроводник является идеальным диамагнетиком с магнитной восприимчивостью χ = -1.

Как возникает этот идеальный диамагнетизм? Оказывается, при помещении сверхпроводящего образца в магнитное поле в поверхностном слое металла возникает стационарный электрический ток, собственное магнитное поле которого противоположно приложенному полю, что в результате и приводит к нулевому значению индукции в толще образца.

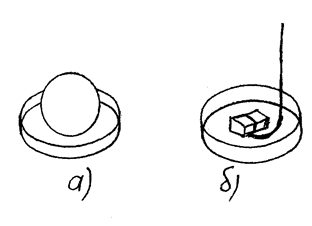
Существование стационарных сверхпроводящих токов можно обнаружить в следующем эксперименте. Если над металлическим кольцом (рис. 7.28.45а), в котором циркулирует такой ток, поместить сверхпроводящую сферу, то на её поверхности индуцируется сверхпроводящий ток. Его возникновение вследствие диамагнитного эффекта приведёт к возникновению сил отталкивания между кольцом и сферой. В результате сфера окажется висящей над кольцом на высоте, определяемой равенством силы отталкивания и весом сферы. Подобный эффект механического отталкивания наблюдается и в том случае, когда над сверхпроводящим кольцом помещается постоянный магнит (рис. 7.28.45б), без видимой поддержки висящий над кольцом, в котором циркулируют индуцированные магнитом незатухающие сверхпроводящие токи. Это явление получило название «гроб Магомета» (по преданию, гроб Магомета висит в пещере без всякой поддержки).

Итак, магнитное поле не проникает в толщу сверхпроводящего образца, но это не относится к поверхностному слою. Более того, именно глубина проникновения поля δ, в котором значение магнитного поля существенно отличается от нуля, является одной из основных характеристик сверхпроводника.

Свойства этого слоя оказываются очень существенными для решения вопроса о возможности получения сверхпроводников с высокими критическими полями.

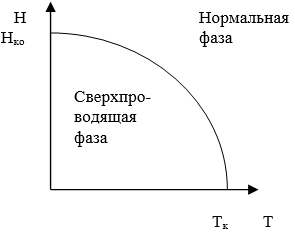
Если мы начнём увеличивать напряжённость внешнего поля, в котором находится образец, имеющий форму бесконечного сплошного цилиндра (ось цилиндра направлена по полю), то при некотором её значении, называемом критическим полем Нк, сверхпроводимость разрушается, и образец переходит в нормальное состояние. Величина Нк зависит от температуры. Чем ближе мы подходим к критической температуре, тем меньше величина Нк и тем легче разрушается состояние сверхпроводимости. На рис. 7.28.46 показано, как с ростом температуры изменяется величина критического поля.

Наиболее устойчиво сверхпроводящее состояние при абсолютном нуле; значение Нк, соответствующее T = 0, максимально. При T = TK величина критического магнитного поля, естественно, обращается в нуль.

Таким образом, металл можно перевести из сверхпроводящего состояния в нормальное, не повышая его температуры.

Казалось бы, в сверхпроводнике при увеличении сверхпроводящего тока можно получить любое требуемое значение индукции магнитного поля. Однако, как только поле сверхпроводящего тока достигнет значения Нк, сверхпроводимость разрушается. Тем не менее, был обнаружен класс веществ, сохраняющих свойство сверхпроводимости в мощных магнитных полях и при сильных токах.

Изотопический эффект. Исследование различных сверхпроводящих изотопов ртути привело к установлению связи между критической температурой и массой изотопов; оказалось, что при изменении массового числа μ от 199,5 до 203,4 наблюдается изменение Тк от 4,185 до 4,140 К . О чём говорит этот результат? Масса изотопа является характеристикой решётки кристалла и может влиять на её свойства. Так, например, частота решёточных колебаний связана с массой ионов соотношением . Сверхпроводимость, которая является свойством электронной системы металла, оказывается связанной ввиду обнаружения изотопического эффекта с состоянием кристаллической решётки. Следовательно, возникновение эффекта сверхпроводимости обусловлено взаимодействием электронов с решёткой кристалла.

Понятие о теории сверхпроводимости. В 1957 г. Бардином, Купером, Шриффером была построена последовательная теория низкотемпературной сверхпроводимости (теория БКШ).

Открытие изотопического эффекта явно указывало на то, что при объяснении явления сверхпроводимости необходимо учитывать взаимодействие электронов с решёткой кристалла. Рассмотрим этот вопрос более подробно.

Напомним, что в обычных металлах электрическое сопротивление возникает из-за рассеяния электронов на фононах, примесных атомах, а также на других дефектах кристаллической решётки. При этом наиболее существенными являются процессы упругого рассеяния, при которых импульс электронов меняется на прямо противоположный и они перебрасываются из правой области кривой распределения в левую, как это показано на рис. 7.23.33) пунктирной стрелкой.

Для того чтобы такие переходы могли происходить, необходимо выполнение двух условий:

а) должны существовать состояния, в которые способны переходить электроны при рассеивании; иначе говоря, уровни энергии, соответствующие этим состояниям, должны принадлежать разрешённой зоне;

б) состояния, в которые могут переходить электроны, не должны быть заняты другими электронами.

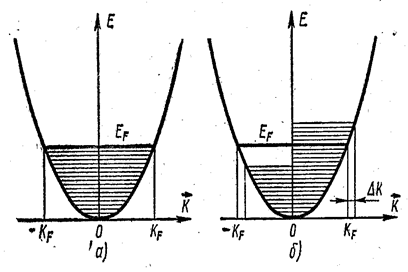
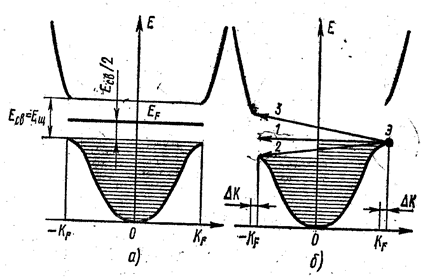
Для нормального металла, имеющего энергетический спектр электронов зоны проводимости, показанный на рис. 7.28.47, оба эти условия выполняются, что и обеспечивает возможность протекания процессов рассеяния.

Можно ли, однако, построить такую модель энергетического спектра электронов проводимости, которая предотвращала бы протекание процессов рассеяния (хотя бы в определённых условиях) даже при наличии фононов, примесных атомов и других «рассеивателей»?

Оказывается, можно. Подобный спектр показан на рис. 7.28.48а. Он отличается от спектра, приведённого на рис. 7.28.47, наличием в зоне проводимости энергетической щели Ещ, посредине которой располагается уровень Ферми. Нижняя часть зоны проводимости заполнена электронами полностью. Верхняя часть, расположенная над щелью, является совершенно пустой. Это напоминает зонную структуру собственного полупроводника при T = 0, который при таком заполнении обладает нулевой электропроводностью. Так как металл сохраняет высокую проводимость и при T ≈ 0 K, то следует допустить, что в отличие от полупроводника, где энергетическая щель (запрещённая зона) не меняет своего положения под действием внешнего поля ε , рассматриваемая щель Ещ в зоне проводимости металла должна двигаться под действием поля ε вместе с электронным распределением, как это показано на рис. 7.28.48б. За время Δt волновой вектор электронов увеличивается на , и щель смещается вместе с распределением вправо на Δk.

Теперь рассмотрим возможность рассеяния, например, электрона Э, располагающегося на верхнем уровне правой полузоны. На рис. 7.28.48б стрелками 1, 2, 3 показаны возможные способы рассеяния:

1 – упругое рассеяние с изменением 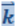на ;

2 – переходы на уровни левой нижней полузоны;

3 – переходы на уровни верхней левой полузоны.

Легко видеть, что переходы 2 запрещены согласно принципу Паули, так как уровни, на которые должны перейти электроны, заняты другими электронами; переходы 3 хотя и разрешены, но для своего осуществления требуют энергии, равной Ещ. Если температура металла достаточно низкая, так что энергия фонона ħω < Eщ, то эти переходы осуществляться не будут.

Таким образом, в металле, электроны проводимости которого обладают энергетическим спектром с «подвижной щелью», показанном на рис. 7.28.48б, процессы рассеяния, ограничивающие электропроводность, в определённых условиях протекать не могут даже при наличии таких рассеивателей, как фононы. Поэтому такой металл может приобрести идеальную проводимость, свойственную сверхпроводникам.

Итак, если бы удалось показать, что у металлов действительно может возникать энергетический спектр электронов проводимости с «подвижной щелью» и если бы были выяснены причины появления такого спектра, то «загадка» сверхпроводимости была бы в значительной степени разгаданной.

В настоящее время разработан ряд методов, позволяющих не только обнаружить такую щель, но и измерить её ширину. Один из них основан на изучении поглощения электромагнитных волн далёкой инфракрасной области металлами. Идея метода в следующем. Если на сверхпроводник направить поток электромагнитных волн и непрерывно изменять их частоту ω, то до тех пор, пока энергия квантов ħω этого излучения остаётся меньше ширины щели Ещ (если таковая, конечно, есть), энергия излучения поглощаться сверхпроводником не должна. При частоте же ωК, для которой ħωK = Ещ, должно начаться интенсивное поглощение излучения, возрастая до его значений в нормальном металле. Измерив ωК, можно определить ширину щели Ещ. Опыты подтвердили факт наличия щели в энергетическом спектре электронов проводимости у известных сверхпроводников. Оказалось, что щель является весьма узкой: Ещ ~ 10-3 - 10-2 эВ; между шириной щели и критической температурой перехода Тк наблюдается связь: чем выше Тк, тем шире щель.

После экспериментального открытия щели встал вопрос о её природе. Напомним: запрещённые зоны в энергетическом спектре полупроводников возникают вследствие взаимодействия электронов с решёткой, создающей в кристалле поле с периодически меняющимся потенциалом. Естественно предположить, что энергетическая щель в зоне проводимости металла, находящегося в сверхпроводящем состоянии, возникает из-за какого-то дополнительного взаимодействия электронов, появляющегося при переходе металла в это состояние. Природа этого взаимодействия состоит в следующем.

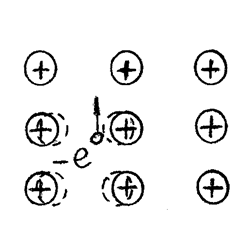
Электрон, движущийся в металле, электрическими силами деформирует - поляризует кристаллическую решётку (рис. 7.28.49). Вызванное таким образом смещение ионов решётки отражается на состоянии другого электрона, поскольку он теперь оказывается в поле поляризованной решётки, несколько изменившей свою периодическую структуру. Таким образом, кристаллическая решётка играет роль промежуточной среды, наличие которой приводит к межэлектронному притяжению.

Наглядно появление сил притяжения можно представить себе следующим образом. В результате деформации решётки электрон оказывается окружённым «облаком» положительного заряда, притягивающегося к электрону. Величина этого положительного заряда может превышать электронный заряд. Тогда такой электрон вместе с окружающим его «облаком» представляет собой положительно заряженную систему, которая будет притягиваться к другому электрону.

При высоких температурах достаточно интенсивное тепловое движение отбрасывает частицы друг от друга, размывает ионную «шубу», что фактически уменьшает силы притяжения. При низких же температурах силы притяжения играют очень важную роль.

Возникновение межэлектронного притяжения не противоречит законам физики. Дело в том, что два электрона, несомненно, отталкиваются друг от друга, если находятся в пустоте. В среде же сила их взаимодействия равна (ε - диэлектрическая проницаемость среды). Если среда такова, что ε < 0, то одноименные заряды будут притягиваться.

Кристаллическая решётка и является той средой, которая делает отрицательной диэлектрическую проницаемость в сверхпроводнике.

Появление дополнительного межэлектронного притяжения может быть описано и в квантовой картине. Рассмотрим металл при T = 0°K. Его кристаллическая решётка не находится в состоянии абсолютного покоя, а совершает так называемые «нулевые» колебания, существование которых связано с квантово-механическим соотношением неопределённостей и соответствует основному состоянию гармонического осциллятора. Электрон, движущийся в кристалле, нарушает режим этих «нулевых» колебаний и переводит решётку в возбуждённое состояние. Обратный переход её сопровождается излучением энергии, которая поглощается другим электроном. Возбуждённое состояние кристаллической решётки описывается с помощью звуковых квантов - фононов. Поэтому описанный выше процесс можно представить себе как излучение фонона электроном, движущимся в решётке, и последующее поглощение фонона другим электроном. Обмен фононами и создаёт в квантовой картине дополнительное притяжение между электронами.

При низких температурах это притяжение у ряда веществ (они и оказываются сверхпроводниками) преобладает над кулоновским электронным отталкиванием.

В этом случае энергетически выгодным становится объединение электронов в связанные пары, которые получили название куперовских пар.

При образовании куперовских пар энергия системы уменьшается на величину энергии связи Есв электронов в паре. Это означает, что если в нормальном металле электроны зоны проводимости при T = 0 K обладали минимальной энергией Еф (см. рис. 7.28.47а), то при переходе в состояние, в котором они связаны в пары, энергия пары уменьшается на Есв, а энергия каждого из них – на Есв / 2 (см. рис. 7.28.48а), так как именно такую энергию надо затратить, чтобы разрушить эту пару. Поэтому между верхним энергетическим уровнем электронов, находящихся в связанных парах, и нижним уровнем нормальных электронов должна существовать щель шириной Есв, которая как раз и необходима для появления сверхпроводимости. Легко убедиться, что эта щель является подвижной, т.е. способной смещаться под действием внешнего поля вместе с кривой распределения электронов по состояниям.

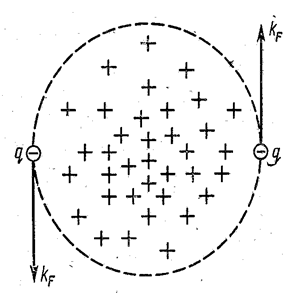
На рис. 7.28.50 представлена схематическая модель куперовской пары. Она состоит из двух электронов (е), движущихся вокруг индуцированного положительного заряда. Каждый электрон, входящий в пару, может обладать большим импульсом и волновым вектором ; пара же в целом (центр масс пары) может при этом покоиться, обладая нулевой скоростью поступательного движения.

Это разъясняет непонятное на первый взгляд свойство электронов, заселяющих верхние уровени заполненной части зоны проводимости при наличии щели. У таких электронов p≈ pF, k ≈ kF, а скорость поступательного движения . Поскольку центральный положительный заряд пары индуцирован самими движущимися электронами, то под действием внешнего поля куперовская пара может свободно перемещаться по кристаллу, а энергетическая щель Ещ смещаться вместе со всем распределением (рис. 7.28.48).

Так как образование пар сопровождается изменением энергии электронов, то связываться в пары могут лишь те электроны, которые способны изменять свою энергию. Таковыми являются только электроны, размещающиеся в узкой полоске, расположенной у уровня Ферми. Грубая оценка показывает, что число таких электронов составляет ~ 10-4 от общего их числа, а ширина полоски по порядку величины равна 10-4pF. Можно показать, что в этих условиях практически будет образовываться лишь одна группа пар – пары, состоящие из электронов, имеющих равные по величине и противоположные по направлению импульсы.

Замечательной особенностью этих пар является их импульсная упорядоченность, состоящая в том, что центры масс всех пар имеют одинаковый импульс, равный нулю, когда пары покоятся, и отличный от нуля, но одинаковый для всех пар, когда пары движутся по кристаллу. Это приводит к довольно жёсткой корреляции движения каждого отдельного электрона с движением всех остальных электронов, связанных в пары.

Электроны движутся наподобие альпинистов, которые связаны друг с другом верёвкой: если один из них выходит из строя благодаря неровности рельефа (обусловленной тепловым движением атомов), то соседи возвращают его обратно. Это свойство делает коллектив куперовских пар мало восприимчивым к рассеянию. Поэтому если пары тем или иным внешним воздействием приведены в упорядоченное движение, то созданный ими электрический ток может существовать в сверхпроводнике сколь угодно долго, даже после прекращения действия того фактора, который его вызвал.

Расчёты показывают, что эффективный диаметр пары L ≈ (10-7 - 10-6) м. В объёме L3, занимаемом парой, размещаются центры масс ~ 106 других таких пар. Возникающее колоссальное перекрытие волновых функций всех пар усиливает квантовый эффект спаривания электронов до макроскопического его проявления.

Таким образом, процесс спаривания электронов является типичным коллективным эффектом. Силы притяжения, возникающие между электронами, не могут привести к спариванию двух изолированных электронов. В образовании пары участвуют по существу как весь коллектив фермиевских электронов, так и атомы решётки. Поэтому и энергия связи (ширина щели Ещ) зависит от состояния коллектива электронов и атомов в целом. При абсолютном нуле, когда все фермиевские электроны связаны в пары, энергетическая щель Ещ достигает максимальной ширины Ещ(0). С повышением температуры появляются фононы, способные сообщить электронам при рассеянии энергию, достаточную для разрыва пары. При низких температурах концентрация этих фононов невелика, вследствие чего и случаи разрыва электронных пар будут редкими. Выход этих пар из «игры» не может, конечно, привести к исчезновению щели для электронов остальных пар, но делает её несколько уже. С дальнейшим повышением температуры концентрация фононов растёт очень быстро, кроме того, растёт и их средняя энергия. Это приводит к резкому увеличению скорости разрыва электронных пар и соответственно к быстрому уменьшению ширины энергетической щели для остающихся пар. При некоторой температуре Тк щель исчезает полностью, и металл переходит в нормальное состояние.

Из приведённых рассуждений следует, что температура перехода металла в сверхпроводящее состояние должна быть тем выше, чем шире щель при абсолютном нуле Ещ(0). Теория БКШ приводит к следующему выражению:

(7.28.128)

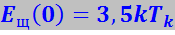
которое подтверждается опытом.

Бесщелевая сверхпроводимость. Если в сверхпроводник вводятся магнитные примеси, то возникает взаимодействие магнитных моментов примеси с электронами, входящими в состав куперовской пары. Спины этих электронов противоположны. Поэтому противоположными оказываются и магнитные моменты электронов, связанных в пары.

Атом примеси различным образом взаимодействует с электронами, связанными в куперовскую пару. Примесь стремится изменить направление магнитного момента у одного из этих электронов, разрушить связанное состояние электронов, что и подтверждается в эксперименте. Даже концентрация магнитных примесей порядка нескольких процентов может разрушить сверхпроводящее состояние.

В присутствии магнитных примесей становится возможным особое состояние так называемой бесщелевой сверхпроводимости. Оказывается, что при введении магнитных примесей щель уменьшается быстрее, чем TK, и при некоторой концентрации n0 энергетическая щель становится равной нулю, в то время как вещество остаётся сверхпроводящим.

С чем же связано появление бесщелевой сверхпроводимости? При концентрации n0 часть куперовских пар оказывается разорванной и возникает картина двухжидкостной модели. Существование «свободных» электронов, образовавшихся при разрыве куперовских пар, приводит к исчезновению энергетической щели. Оставшиеся же куперовские пары обеспечивают равенство нулю электрического сопротивления.

Явление бесщелевой сверхпроводимости оказывается возможным не только в присутствии магнитных примесей. Всякое поле, действующее различным образом на электроны, входящие в состав куперовской пары и стремящееся разрушить сверхпроводящее упорядочение, может привести к состоянию бесщелевой сверхпроводимости. Например, это состояние возникает в тонких плёнках в присутствии внешнего магнитного поля, в плёнках с током, близким к критическому и т.д.

Возможность возникновения бесщелевой сверхпроводимости указывает на то, что существование щели не является обязательным условием проявления сверхпроводящего состояния. Главное – это наличие связанного электронного состояния, куперовских пар; это состояние может проявлять сверхпроводящие свойства и в отсутствие энергетической щели.

Сверхпроводимость в полупроводниках. В полупроводниках электронная концентрация меньше, чем в металлах, и это обстоятельство препятствует, конечно, образованию связанного состояния, характерного для сверхпроводящей фазы. Однако, с другой стороны, полупроводники характеризуются обычно большим значением диэлектрической проницаемости ε. В связи с этим кулоновское отталкивание, препятствующее межэлектронному притяжению, оказывается ослабленным в ε раз. Эти соображения не исключают возможности наблюдения сверхпроводимости у полупроводников. Поиски таких веществ привели в 1963 г. к открытию первых сверхпроводящих полупроводников. Ими оказались GeTe (TK ~ 0,08 K) и SrTiO3 (TK ~ 0,3 K) и др. Под высоким давлением (~ 100 к/бар) была обнаружена сверхпроводимость Ge и Si.

Эффекты Джозефсона. В 1962 г. английским физиком-теоретиком Джозефсоном была предсказана возможность обнаружения двух необычных эффектов. Эффекты эти вскоре были экспериментально открыты.

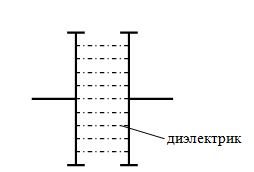
Различают стационарный и нестационарный эффекты Джозефсона. Первый из них состоит в возможности протекания постоянного тока через туннельный контакт (рис. 7.28.51), образованный двумя сверхпроводниками, разделёнными тонким слоем (~ 10-9 м) диэлектрика. Существенно, что этот сверхпроводящий ток протекает через барьер, характеризующийся нулевой разностью потенциалов. Величина плотности этого тока определяется соотношением

,

где φ - разность фаз волновых функций электронных пар в первом и втором сверхпроводнике.

Если к контакту приложить постоянную разность потенциалов, то через него потечёт переменный сверхпроводящий ток. Этот переменный ток будет излучать электромагнитные волны, и это излучение наблюдается на опыте. За счёт чего возникает излучение? Электронные пары проходят через диэлектрический слой и приобретают при этом энергию 2eU (U – разность потенциалов, приложенная к контакту). В обычном металле эта энергия была бы необходима для преодоления сил сопротивления. При протекании же сверхпроводящего тока не требуется затрат энергии, и полученная электронной парой порция 2eU излучается в виде кванта с частотой . Тот факт, что излучение происходит именно с такой частотой, можно рассматривать как экспериментальное подтверждение правильности теоретического представления о существовании в сверхпроводниках связанных электронных пар.

Возможна ли сверхпроводимость при высоких температурах? Существует два главных направления поисков веществ с высокими Тк. Первое из них базируется на использовании возможностей рассмотренного механизма сверхпроводимости, второе связано с поиском новых высокотемпературных механизмов сверхпроводимости.

Для температуры Тк, при которой обычные сверхпроводники переходят в нормальное состояние, в теории получено соотношение:

(7.28.129)

где ħϖ - средняя энергия фононов, по порядку величины равная ( - температура Дебая);

ρ - константа связи, определяющая межэлектронное притяжение.

Из (7.28.129) видно, что значения Тк не могут превосходить , экспоненциальный множитель приводит к уменьшению Тк примерно на порядок, что и соответствует наблюдаемым низким значениям температур, при которых отмечается эффект сверхпроводимости.

Обычный механизм сверхпроводимости, как отмечалось, связан с деформацией и поляризацией кристаллической решётки электронной системой металла. Таким образом, малость Тк связана с особенностями кристаллической решётки. Если изменить структуру кристаллической решётки так, чтобы электроны сильнее связывались друг с другом, то можно повысить Тк и с помощью обычного механизма электронно-ионного взаимодействия.

Но если говорить о высокотемпературной и комнатно-температурной сверхпроводимостях, то в этом случае может помочь только поиск новых механизмов сверхпроводимости.

Притяжение электронов, приводящее к сверхпроводимости, создаётся, как только что отмечено, за счёт промежуточной среды. Возникает вопрос: а нельзя ли найти другую среду, которая обеспечила бы более сильное межэлектронное притяжение?

Как показывают современные исследования, таких сред может быть предложено достаточно много. Рассмотрим некоторые из них.

Б.Т. Гейликманом были исследованы две возможности установления сверхпроводящего состояния. Первая из них реализуется, по-видимому, в сплавах, содержащих так называемые переходные металлы.

Необходимым условием сверхпроводящего состояния, согласно теории, является наличие перекрывающихся энергетических зон (рис. 7.28.52). Электроны, принадлежащие более узкой зоне, менее подвижные и характеризуются большей эффективной массой т*.

Электроны, относящиеся к зонам а и в, отличаются как своими эффективными массами, так и волновыми функциями, описывающими их квантово-механическое состояние. В обеих зонах имеются незаполненные энергетические уровни, благодаря чему становятся возможными электронные переходы. Кулоновское взаимодействие между электронами, принадлежащими различным зонам, и приводит к образованию куперовских сверхпроводящих пар. Появление дополнительного межэлектронного взаимодействия, например, в зоне а (условия для установления сверхпроводящего состояния в широкой зоне оказываются более благоприятными) можно представить себе следующим образом. Электрон, принадлежащий зоне а, посредством кулоновских сил вызывает переход в-электрона в возбуждённое состояние.

Обратный переход в-электрона изменяет состояние другого а-электрона, что в результате означает появление дополнительного межэлектронного взаимодействия в зоне а. Система станет сверхпроводящей, если определяемое указанным механизмом притяжение окажется более интенсивным, чем обычное кулоновское отталкивание а-электронов.

Рассмотренный механизм аналогичен обычному, однако роль кристаллической решётки играют электроны, принадлежащие к узкой зоне. Их эффективная масса, как известно, значительно превосходит массу свободного электрона. Таким образом, можно сказать, что почти свободные а-электроны, принадлежащие широкой зоне, образуют сверхпроводящую систему благодаря взаимодействию с «тяжёлыми» электронами.

Выше мы приводили соотношение TK ~ μ-1/2, связывающее критическую температуру и массу иона. При новом, электронном, механизме сверхпроводимости в этом соотношении будет фигурировать масса в-электрона: TK ~ m*-1/2, что в силу неравенства μ >> m* делает возможным сверхпроводящее состояние с более высокой Тк. Соответствующий расчёт даёт, что в сплавах с перекрывающимися зонами может наблюдаться сверхпроводимость, сохраняющаяся до температур порядка 102-103 K.

Другая возможность может быть рассмотрена на примере системы, представляющей собой сплав металла с неметаллическим веществом. Электроны проводимости могут перемещаться по всему металлу. Вторая же группа частиц образована электронами неметаллических включений. Взаимодействие этих двух групп электронов и приводит к возможности возникновения сверхпроводимости в металле.

Новый механизм сверхпроводимости, не связанный со взаимодействием электронов с решёткой кристалла и могущий привести к высоким значениям Тк, был предложен В.Л. Гинзбургом. Если на поверхность металлического образца нанести диэлектрический или мономолекулярный слой, то электронные переходы в такого рода покрытии могут привести к появлению сверхпроводимости электронов металла.

Рассмотренный поверхностный эффект может привести к заметному повышению Тк в случае, когда покрытие наносится на достаточно тонкий металлический слой. Наиболее сильно он может проявиться в сложной структуре, называемой «сэндвичем» и состоящей из тонкой металлической плёнки и прилегающих к ней с обеих сторон слоёв диэлектрика.

В последнее время усилился интерес к изучению физических свойств органических соединений. Проводящий органический кристалл в принципе может, конечно, обнаруживать и сверхпроводящие свойства. Сверхпроводящее состояние в этих кристаллах может возникнуть за счёт взаимодействия π-электронов с неколлективизированными электронами и т.д.

Таким образом, существуют достаточно убедительные основания, позволяющие рассчитывать на создание в ближайшее время образцов, обнаруживающих сверхпроводимость при высоких температурах. А пока исследование керамик позволило в соединениях оксида иттрия, бария и меди получить критические температуры TK = 90 K. Наивысшая температура TK = 135 K достигнута для HgBa2Ca2Cu3O8+x без давления; под довольно большим давлением для него уже TK = 164 K.

В 1989 г. был открыт новый класс сверхпроводников, носителями заряда у которых являются электроны. Это открытие даёт надежду на получение сверхпроводящих материалов с более высокими критическими температурами и создание теоретического объяснения высокотемпературной сверхпроводимости.

Применение сверхпроводимости. Если раньше сверхпроводящие вещества в основном были предметом исследования, то в последнее время всё больше возрастает роль сверхпроводимости как метода, с помощью которого получаются интересные результаты в различных областях физики и техники.

Много исследований посвящается вопросу об использовании сверхпроводников при создании вычислительных машин. Сверхпроводящий ток является незатухающим. Это позволяет использовать его в качестве идеального запоминающего устройства, хранящего большие и легко считываемые запасы информации.

Скорость «вспоминания» сверхпроводящих устройств значительно превышает возможности человеческого мозга. Они в состоянии всего лишь за 10-6 c выбрать нужную информацию из 1011 её единиц.

В вычислительной технике используется двоичная система. Двойственность сверхпроводников (они могут находиться или в нормальном, или в сверхпроводящем состоянии), быстрота их перехода под действием температуры или магнитного поля из одного состояния в другое позволяют использовать сверхпроводники в качестве элементов вычислительных машин. Сверхпроводники используются и в качестве переключающих устройств, работающих с очень высокой скоростью при малых затратах мощности.

Одно из таких устройств – так называемый проволочный криотрон. Он состоит из проволоки, сделанной, например, из свинца или тантала, по которой протекает сверхпроводящий ток. Эта проволока называется клапаном. На неё намотана более тонкая проволока из ниобия. Катушка, образованная этим тонким проводом, называется управляющей. При протекании в ней достаточно большого тока сверхпроводимость в клапане разрушается. Ниобий был выбран в качестве материала, из которого изготавливается управляющий провод, по той причине, что сверхпроводимость сохраняется в нём при достаточно сильных магнитных полях. Критические же поля свинца или тантала, образующих клапан, являются весьма малыми, и сверхпроводимость разрушается в них при пропускании в ниобиевой катушке достаточно слабого тока. Сопротивление в клапане меняется при этом скачком от нуля до некоторого конечного значения. Это соответствует размыканию цепи. Уменьшение тока в управляемом проводе снова восстанавливает сверхпроводящее состояние свинца или тантала.

Скорость переключения в криотронах достигает двух наносекунд. Высокая скорость в сочетании с простотой устройства и лежит в основе использования сверхпроводящих криотронов в вычислительной технике.

Сверхпроводник, в толщу которого не проникает магнитное поле, всегда окружён магнитной «подушкой». Эффект механического отталкивания, о котором мы говорили выше («гроб Магомета»), используется в настоящее время для создания опор без трения. Такие подвесы могут использоваться в гироскопах, моторах и ряде других устройств.

Принцип механического отталкивания положен в основу создания электрических машин с к.п.д., равным 100%. В этих машинах вращающаяся часть – ротор – выполнена в виде шестиугольного сверхпроводящего стаканчика. Два магнита, вращающиеся по окружности статора, отталкивают от себя магнитной «подушкой» сверхпроводящий ротор. Последний приходит во вращение, скорость которого доходит до 20000 об/мин.

Этот же принцип механического отталкивания используется в поездах на «магнитной подушке».

Многообразно применение сверхпроводимости в технике сильных токов: линии электропередачи и генераторы для выработки электроэнергии; накопители, предназначенные для «сброса» электроэнергии в сеть в часы «пик»; сверхпроводящие магниты.

При этом, если сверхпроводящим линиям электропередачи и другим устройствам ещё только предстоит завоёвывать место под солнцем, то в отношении электромагнитов, способных создавать сверхсильные поля, вопроса о достоинствах применения сверхпроводников даже не возникает. Например, чтобы с помощью обычного соленоида создать поле порядка 10 Тл, необходима электрическая мощность тока около 5000 кВт. Такой ток выделяет столь значительную тепловую мощность, что для её отвода нужно прокачивать через соленоид не менее нескольких кубометров воды в минуту.

Если же для этой цели использовать магнит со сверхпроводящей обмоткой, то в принципе энергия нужна только на первом этапе – для наведения в нём тока. Затем магнит вообще можно отключить от источника питания.

Мы кратко рассказали здесь о некоторых областях применения сверхпроводников. Всё ли мы охватили? Конечно, нет.

к к к