ФИЗИКА

7.27. Электронно-дырочный (p-n) переход

Основным элементом современной полупроводниковой электроники является контакт двух примесных полупроводников с различным типом проводимости. Такой контакт называют электронно-дырочным переходом или р-n-переходом. Рассмотрим кратко его свойства.

Получение р-n-перехода. Получить р-n-переход непосредственным соприкосновением двух полупроводников практически невозможно, так как их поверхность, как бы тщательно она не была очищена, содержит огромное количество примесей, загрязнений и всевозможных дефектов, резко меняющих свойства полупроводников. Поэтому успех в освоении р-n-перехода был достигнут лишь тогда, когда научились делать его в виде внутренней границы в монокристаллическом полупроводнике.

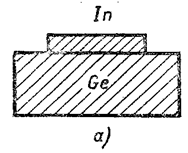
К настоящему времени разработано много методов получения р-n-перехода. В качестве примера мы рассмотрим только один из них – метод сплавления, сущность которого состоит в следующем. Кристалл германия n-типа с положенным на него кусочком индия In (рис. 7.27.39а) выдерживается в печи при температуре 500-600°C в атмосфере водорода или аргона. При этом

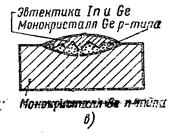
In расплавляется и растворяет в себе Ge (рис. 7.27.39в). При медленном охлаждении из расплава выпадает Ge, насыщенный In. Он кристаллизуется в форме монокристалла, ориентированного одинаково с монокристаллом подложки. Так как германий, содержащий индий, обладает р-проводимостью, то на границе закристаллизовавшегося расплава и монокристалла германия, обладающего n-проводимостью, образуется р-n-переход (рис. 7.27.39в). Капля индия на поверхности германия используется в качестве омического контакта.

Равновесное состояние р-n-перехода. Пусть внутренней границей раздела двух областей полупроводника с различным типом проводимости

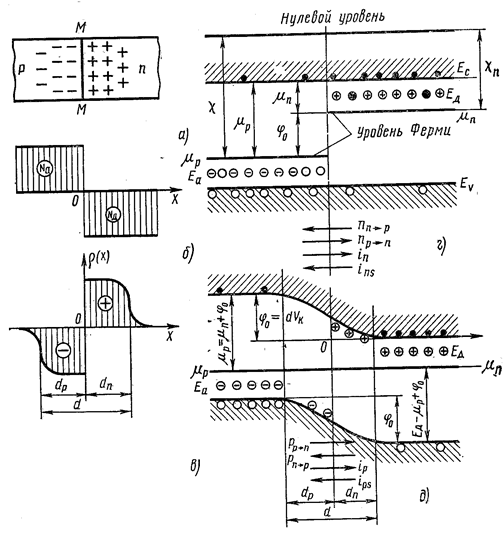
является плоскость ММ (рис. 7.27.40а): слева от неё находится полупроводник р-типа, например р-германий, с концентрацией акцепторов Na; справа – полупроводник n-типа (n-германий) с концентрацией доноров NД. Для простоты будем считать, что NA = NД и равно, например, 1022 м-3. На рис. 7.27.40б показано изменение концентрации акцепторных и донорных атомов при перемещении вдоль оси Х, перпендикулярной плоскости ММ. В точке О, лежащей в этой плоскости, Na скачкообразно падает до нуля, NД скачкообразно увеличивается от нуля до NД.

Для n-области основными носителями являются электроны, для р-области – дырки. Основные носители возникают почти целиком за счёт ионизации донорных и акцепторных примесей. При не слишком низких температурах эти примеси ионизированы практически полностью, вследствие чего концентрацию электронов в n-области (nn0) можно считать практически равной концентрации донорных атомов NД (nn0 ≈ NД), а концентрацию дырок в р-области (pp0) можно считать равной концентрации акцепторных атомов Na (pp0 ≈ Na).

Помимо основных носителей, эти области содержат неосновные носители: n-область – дырки (pn0), р-область – электроны (np0).

Их концентрацию можно определить из закона действующих масс:

,

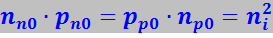где ni - концентрация носителей в собственном полупроводнике. При nn0 = pp0 = 1022 м-3 и ni = 1019 м-3 получим

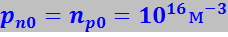
Из этих соотношений видно, концентрация дырок в р-области на шесть порядков выше концентрации их в n-области; точно так же концентрация электронов в n-области на шесть порядков выше их в р-области. Такое различие в концентрации однотипных носителей в контактирующих областях проводника приводит к возникновению диффузионных потоков электронов из n-области в р-область (nn→p) и диффузионного потока дырок из р-области в n-область (pp→n). При этом область n, из которой диффундировали электроны, заряжается положительно, область р, из которой диффундировали дырки, - отрицательно. Это заряжение приводит соответственно к понижению всех энергетических уровней, в том числе и уровня Ферми в n-области и повышению их в р-области. Перетекание электронов справа налево и дырок слева направо происходит до тех пор, пока постепенно поднимающийся уровень Ферми в р-области (μp) не установится на одной высоте с постепенно опускающимся уровнем Ферми в n-области (μn). С установлением этих уровней на одной высоте между n- и р-областями устанавливается равновесие, при котором поток электронов из n-области в р-область (nn→p) уравновешивается потоком электронов из р-области в n-область (np→n), а поток дырок из р- в n-область (pp→n) уравновешивается потоком дырок из n- в р-область (pn→p):

(7.27.118)

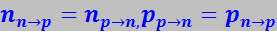
Уход электронов из приконтактного слоя n-области приводит к возникновению в этом слое неподвижного положительного объёмного заряда ионизированных атомов донорной примеси. Обозначим толщину этого слоя через dp. Уход дырок из приконтактного слоя р-области вызывает появление в этом слое неподвижного отрицательного объёмного заряда, локализованного на атомах акцепторной примеси; обозначим толщину этого слоя через dp. Между этими слоями возникает контактная разность потенциалов VK, создающая в р-n-переходе потенциальный барьер φ0, препятствующий переходу электронов из n- в р-область и дырок из р- в n-область.

(7.27.119)

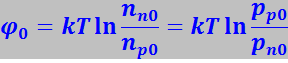
Из (7.27.119) видно, что φ0 тем выше, чем больше отношение концентрации основных носителей в данной области полупроводника к концентрации этих носителей в другой области полупроводника, в которой они являются неосновными. При nn0 = 1022м-3, np0 = 1016м-3 и Т = 300К, φ ≈ 0,45 эВ.

Из сравнения рис. 7.27.40 г, д легко видеть, что

Выпрямляющие свойства р-n-перехода. Основное свойство р-n-перехода – способность выпрямлять переменный электрический ток. Рассмотрим это свойство более подробно.

Токи, текущие через р-n-переход в равновесном состоянии. В равновесном состоянии через р-n-переход проходят потоки основных и неосновных носителей (см. рис. 7.27.40в). Обозначим плотность токов, отвечающих потоку nn→p через jn, потоку np→n- через jns, потоку pp→n- через jp, потоку pn→p- через jps.

В соответствии с (7.27.118) можно записать:

.

Складывая левые и правые части этих равенств, найдём:

.

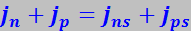Левая часть полученного соотношения выражает составляющую плотности j полного тока, образованного основными носителями, правая часть – неосновными носителями. Полный ток, текущий через равновесный р-n-переход, равен, очевидно, нулю:

(7.27.120)

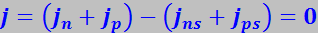
Вычислим jns и jps. Для этого выделим на левой границе 1 р-n-перехода (рис. 7.27.41) единичную площадку s и построим на ней цилиндр с образующей, равной Ln /τn, где Ln- диффузионная длина электронов в р-области; τn- среднее время их жизни. Так как диффузионная длина представляет собой среднее расстояние, на которое диффундирует носитель за время своей жизни, то отношение Ln /τn выражает, очевидно, среднюю скорость диффузии электронов из глубины р-области, где их концентрация равна np0, к границе 1, где они подхватываются контактным полем εK и перебрасываются в n-область. Число электронов, заключённых в выделенном цилиндре, равно объёму цилиндра Ln /τn, умноженному на концентрацию электронов np0, т.е. . Все эти электроны в течение 1 с пройдут через единичную площадку s и будут переброшены в n-область, образуя ток плотностью

(7.27.121)

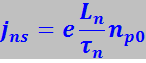
Точно так же можно вычислить и jps, строя цилиндр на границе 2 р-n-перехода

(7.27.122)

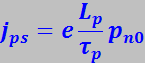
Таким образом, для равновесного состояния р-n-перехода

(7.27.123)

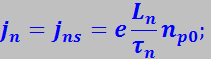
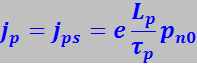
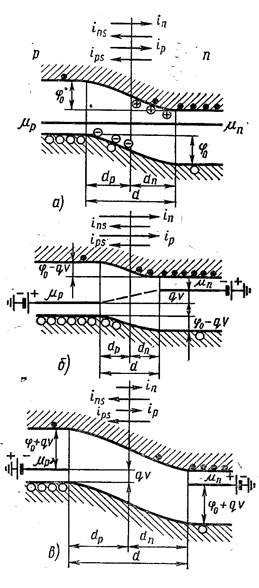
Прямой ток. Приложим к р-n-переходу, находившемуся в равновесии (рис. 7.27.42а), внешнюю разность потенциалов в прямом направлении (рис. 7.27.42б). Эта разность потенциалов вызывает понижение потенциального барьера для основных носителей до φ0 - qV. Поэтому поток дырок из р- в n-область (pp→n) увеличится в eeV / kT раз, что приведёт к увеличению в eeV / kT раз плотности токов основных носителей jn и jp, которые станут соответственно равными:

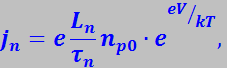
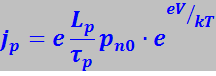
В то же время плотности токов неосновных носителей jns и jps, величина которых не зависит от величины потенциального барьера, останутся неизменными.

Поэтому полный ток, текущий через р-n-переход будет равен

(7.27.124)

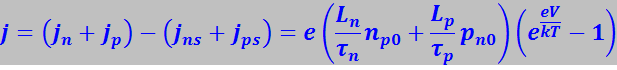
Этот ток называют прямым.

Обратный ток. Приложим теперь к р-n-переходу внешнюю разность потенциалов в обратном направлении, подключив к р-области отрицательный полюс источника напряжения, к n-области – положительный. Под действием этой разности потенциалов потенциальный барьер повысится, что вызовет уменьшение в eeV / kT раз потока основных носителей nn→p и pp→n и плотности токов jn и jp.

С учётом этого плотность тока через р-n-переход будет равна

(7.27.125)

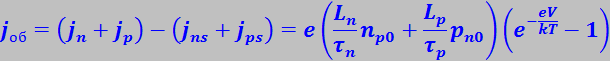
Этот ток называют обратным.

Вольт-амперная характеристика. Объединяя (7.27.124) и (7.27.125), получим

(7.27.126)

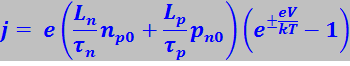
Это соотношение представляет собой уравнение вольт-амперной характеристики р-n-перехода; знак «+» относится к прямому направлению V, знак «-» - к обратному (запорному).

Проанализируем (7.27.126). При приложении внешней разности потенциалов V в запорном направлении с увеличением V экспонента , а скобка . Вследствие этого плотность тока jоб стремится к предельному значению 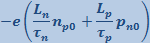, абсолютную величину которого

(7.27.127)

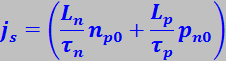
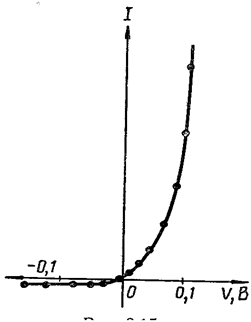
называют плотностью тока насыщения. Практически она достигается уже при eV ≈ kT, т.е. при V ≈ 0,1B. Из (7.27.127) видно, что js определяется потоком через р-n-переход неосновных носителей и является небольшой величиной.

При приложении к р-n-переходу внешней разности потенциалов в прямом направлении сила тока через переход растёт по экспоненте и уже при незначительных напряжениях достигает большого значения.

На рис. 7.27.43 показан график вольт-амперной характеристики р-n-перехода, отвечающий уравнениям (7.27.126) и (7.27.127). Он вычерчен в разном масштабе для прямой и обратной ветвей. Отношение Iпр / Iоб ~ 109. Это свидетельствует о том, что р-n-переход обладает практически односторонней проводимостью.

к к к