ФИЗИКА
Законы идеальных газов были установлены экспериментально. Покажем, что все эти законы могут быть получены из приведённых выше уравнений кинетической теории газов.
Закон Бойля-Мариотта. Если температура газа поддерживается постоянной, то правая часть уравнения (2.2.18) оказывается величиной постоянной, так что
(2.2.20)
.
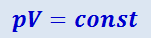Эта формула, которую называют уравнением изотермы, и выражает закон Бойля-Мариотта, согласно которому при постоянной температуре сжатие и расширение газа, т.е. изменение его объёма и давления, происходят так, что произведение давления на объём остаётся величиной постоянной. Графически зависимость p от V для различных температур изображена на рис. 2.2.4. Из формулы (2.2.20) видно, что эти кривые, называемые изотермами, представляют собой гиперболы.
Рис. 2.2.4 |
Закон Бойля-Мариотта показывает, как изменяется объём газа с изменением его давления при постоянной температуре и, конечно, при неизменной массе.
Законы Гей-Люссака:
1) объём данной массы газа при постоянном давлении изменяется линейно с температурой:
(2.2.21)
;
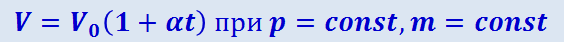2) давление данной массы газа при постоянном объёме изменяется линейно с температурой:
(2.2.22)
.
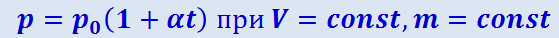В этих уравнениях t – температура по шкале Цельсия, p0 и V0 - давление и объём при 0 °C, коэффициент α = 1/273,15 K-1.
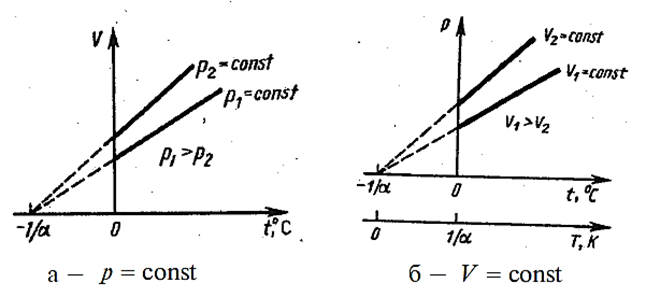
Процесс, протекающий при постоянном давлении, называется изобарным. На диаграмме в координатах V, t (рис. 2.2.5 а) этот процесс изображается прямой, называемой изобарой. Процесс, протекающий при постоянном объёме, называется изохорным. На диаграмме в координатах p, t (рис. 2.2.5 б) он изображается прямой, называемой изохорой.
Рис. 2.2.5 |
Из (2.2.21) и (2.2.22) следует, что изобары и изохоры пересекают ось температур в точке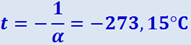 
, определяемой из условия 1 + αt = 0. Если перенести начало отсчёта в эту точку, то происходит переход к шкале Кельвина (см. рис. 2.2.5 б), откуда
.
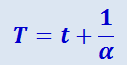Вводя в формулы (2.2.21) и (2.2.22) термодинамическую температуру, законам Гей-Люссака можно придать более удобный вид:
(2.2.23)
,
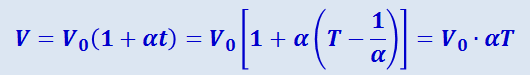(2.2.24)
.
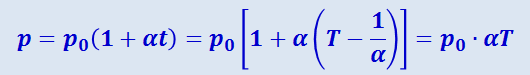Отсюда
(2.2.25)
,
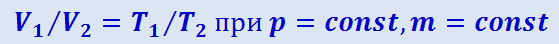(2.2.26)
,
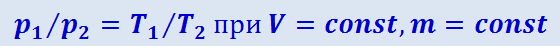где индексы 1 и 2 относятся к произвольным состояниям, лежащим на одной изобаре или изохоре.
Закон Авогадро. Из уравнения состояния идеальных газов непосредственно следует и закон Авогадро, согласно которому при одинаковых давлениях и температурах в равных объёмах любого газа содержится одинаковое число молекул. Действительно, пусть мы имеем два одинаковых объёма двух различных газов при одинаковых давлениях и температурах. Для каждого из них можно написать уравнение состояния в форме (2.2.15)
,
где N1 и N2 - число молекул в каждом из объёмов. Из этих равенств следует, что
.
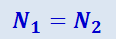Это и есть закон Авогадро.
Из этого закона с очевидностью следует, что и, наоборот, различные газы, но содержащие одинаковое число молекул, будут при одинаковых давлениях и температурах занимать одинаковые объёмы. Поэтому моль любого газа при данных давлении и температуре занимает одинаковый объём. В частности, при 0°C и при давлении в 1 атм моль любого газа занимает объём V0 = 22,41 ⋅ 10-3 м3/моль.
Закон Дальтона. Пусть в сосуде объёмом V имеется находящаяся в состоянии теплового равновесия смесь различных газов, не реагирующих химически друг с другом. Для такой смеси уравнение состояния имеет вид
,
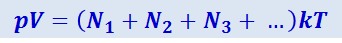где N1, N2, N3... - числа молекул соответствующих компонентов смеси.
Очевидно, что
,
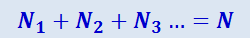где N – общее число молекул в сосуде.
Давление газа
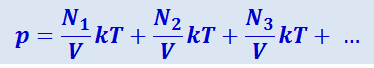
Это выражение показывает, что каждая группа молекул оказывает давление, не зависящее от того, какое давление оказывают другие молекулы. Это обусловлено тем, что в идеальном газе между молекулами нет взаимодействия, молекулы «не знают» о существовании других молекул.
Выражения
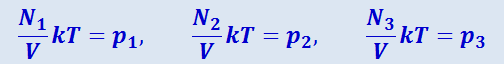
представляют собой давления каждого из компонентов смеси, занимающей объём V, т.е. p1, p2, p3... являются парциальными давлениями компонентов смеси.
Напомним, что парциальным давлением какого-либо газа – компонента газовой смеси - называется давление, которое оказывал бы этот газ, если бы он один занимал весь объём, занимаемый смесью.
Таким образом,
,
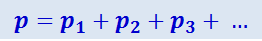т.е. давление смеси газов равно сумме парциальных давлений её компонентов. Это и есть содержание закона Дальтона, который, очевидно, справедлив только для идеальных газов, с невзаимодействующими молекулами.
Пользуясь основными результатами кинетической теории газов, мы, таким образом, получили законы, управляющие поведением газов, установленные экспериментально задолго до того, как была развита теория. Это в какой-то мере подтверждает правильность теории, позволяет считать её проверенной опытом. Это указывает также на то, что газовые законы, рассмотренные выше, относятся только к идеальным газам, что, вообще говоря, не было известно до появления кинетической теории газов.
к к к