ФИЗИКА
7.17. Функция распределения для вырожденного газа ферминов
Она имеет следующий вид:
(7.17.78)
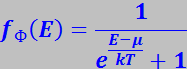
где μ - химический потенциал вырожденного электронного газа, который чаще называют уровнем Ферми.
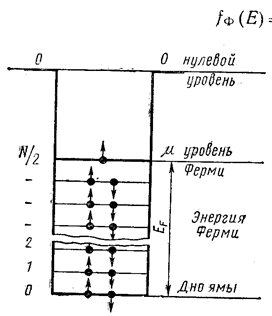
Функцию (7.17.78) называют функцией Ферми-Дирака. Наглядное представление о ней можно получить, рассматривая вырожденный электронный газ в металлах при абсолютном нуле. Металл для свободных (валентных) электронов является своеобразной потенциальной ямой, выход из которой требует затрат работы по преодолению сил связи, удерживающих электроны в металле. На рис. 7.17.27 представлена схема такой потенциальной ямы.
Рис. 7.17.27 |
Горизонтальными линиями показаны энергетические уровни, которые могут занимать электроны. В соответствии с принципом Паули на каждом таком уровне могут разместиться два электрона с противоположными спинами. Если электронный газ содержит N электронов, то последним занятым окажется уровень N/2. Этот уровень и называется уровнем Ферми для вырожденного электронного газа. Он соответствует максимальной кинетической энергии Eф, которой может обладать электрон в металле при абсолютном нуле. Её называют энергией Ферми.
Таким образом, при абсолютном нуле все состояния с энергией Е < Eф заняты электронами, состояния с энергией Е > Eф свободны. Иначе говоря, при T = 0K вероятность заполнения электронами состояний с энергией Е < Eф равна 1, вероятность заполнения Е > Eф равна нулю:
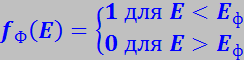
Рис. 7.17.28 |
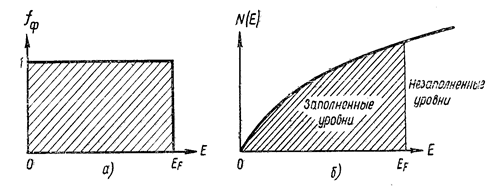
На рис. 7.17.28а показан график функции распределения Ферми-Дирака при абсолютном нуле. Умножая единицу на число состояний, получим функцию распределения Ферми-Дирака при абсолютном нуле:
(7.17.79)
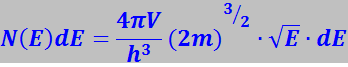
График этой функции показан на рис. 7.17.28б.
Интегрируя (7.17.79) в пределах от 0 до Еф, получим 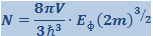 , откуда
, откуда
(7.17.80)
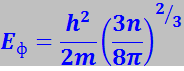
где ![]() - концентрация электронного газа в металле.
- концентрация электронного газа в металле.
Зная Eф, можно определить среднюю энергию электронов при абсолютном нуле
(7.17.81)
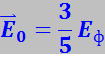
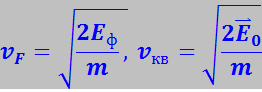
Зная Eф и ![]() , можно найти максимальную νF и среднеквадратичную νкв скорости движения свободных электронов в металле при абсолютном нуле:
, можно найти максимальную νF и среднеквадратичную νкв скорости движения свободных электронов в металле при абсолютном нуле:
(7.17.82)
Из соотношения Eф = kTф можно найти температуру Ферми Tф:
(7.17.83)
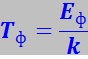
где k – постоянная Больцмана.
Tф показывает, при какой температуре обычный невырожденный газ с массой молекул, равной массе электрона, имел бы энергию теплового движения kT, равную энергии Еф.
Влияние температуры на распределение Ферми-Дирака. С повышением температуры электроны подвергаются тепловому возбуждению и переходят на более высокие энергетические уровни, вследствие чего меняется характер их распределения по состояниям.
Однако в интервале температур, в котором энергия теплового движения kT остаётся значительно ниже энергии Ферми
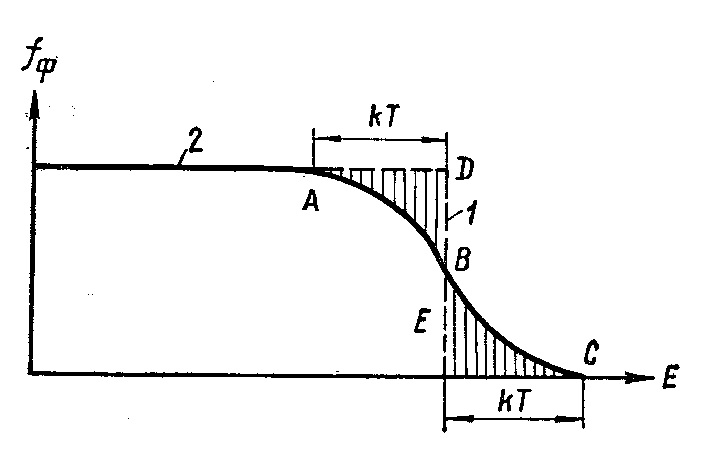
E = Еф, тепловому возбуждению могут подвергаться электроны лишь узкой полосы kT, непосредственно расположенной у уровня Ферми (на рис. 7.17.29 возбуждённые состояния показаны штриховкой). Электроны более глубоких уровней остаются практически незатронутыми.
Рис. 7.17.29 |
В результате теплового возбуждения часть электронов, имевших энергию, меньшую Еф, переходит на уровни с энергией, большей Еф. Из рис. 7.17.29 видно, что повышение температуры вызывает размытие распределения на глубину kT и появление «хвоста» распределения ВС. Чем выше температура, тем более существенному изменению подвергается функция распределения. Сам «хвост» ВС описывается уже максвелловским распределением.
На рис. 7.17.29 заштрихованные площадки пропорциональны числу электронов, покидающих состояния с энергией E < Еф(площадка АДВ) и переходящих на уровни, расположенные выше Еф (площадка ЕфВС). По величине эти площадки равны, так как выражают одно и то же число электронов. Оценить это число можно по соотношению
(7.17.84)
![]()
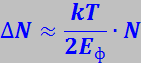
При комнатной температуре kT ≈ 0,025 эВ, Еф = 3-10 эВ, поэтому ![]() ; при
; при ![]() .
.
Таким образом, во всём диапазоне температур, в котором электронный газ в металле является вырожденным, его распределение мало отличается от распределения при абсолютном нуле.
С невырожденным электронным газом приходится иметь дело в собственных (беспримесных) и в слаболегированных полупроводниках. Концентрация свободных электронов в таких полупроводниках значительно ниже, чем в металлах, и колеблется от 1016-1019 до 1023-1024 м-3. При таких концентрациях выполняется условие невырожденности (7.17.66) и электронный газ оказывается невырожденным.
к к к