ФИЗИКА

К содержанию

2.2.3. Уравнение состояния идеального газа

Состояние идеального газа определяется тремя параметрами: давлением р, под которым находится газ, его температурой Т и объёмом V, занимаемым определённой массой газа. Перечисленные величины не являются независимыми. Каждая из них является функцией двух других. Уравнение, связывающее все три величины для данной массы газа, называется уравнением состояния и может быть в общем виде записано так:

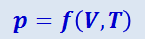
Это значит, что состояние газа определяется только двумя параметрами (например, давлением и объёмом, давлением и температурой или, наконец, объёмом и температурой), третий параметр однозначно определяется двумя другими. Если уравнение состояния известно в явном виде, то любой параметр можно вычислить, зная два других.

Для идеальных газов уравнение состояния легко получить из основных уравнений кинетической теории (2.2.10) и (2.2.13).

В самом деле, подставив в (2.2.10) вместо средней кинетической энергии молекул её выражение из (2.2.13), получим:

(2.2.14)

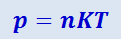
Если в объёме V содержится N частиц, то 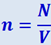; подставив это выражение в (2.2.14), будем иметь:

(2.2.15)

.

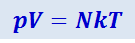Это уравнение и является уравнением состояния идеальных газов. Его, однако, полезно преобразовать так, чтобы в него вместо недоступного прямому измерению числа частиц N входила легко измеряемая величина массы газа т.

Если разделить число молекул N в данной массе газа т на число Авогадро, то получим число молей в данной массе газа. Эту же величину можно получить, разделив массу газа т на его молекулярную массу М. Таким образом:

,

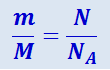отсюда

(2.2.16)

.

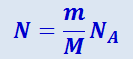Подставим (2.2.16) в (2.2.15). Тогда уравнение состояния примет вид:

(2.2.17)

.

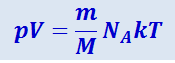В это уравнение входят две универсальные константы NA = 6,02 ⋅ 1023 моль-1 и k = 1,38 ⋅ 10-23 Дж/град. Произведение этих констант, очевидно, тоже является универсальной константой. Она обозначается R:

.

Заменив в (2.2.17) NA ⋅ k универсальной газовой постоянной, получим:

(2.2.18)

.

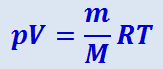Представленное в таком виде уравнение состояния идеального газа часто называют уравнением Клайперона-Менделеева. Величина , входящая в это уравнение, представляет собой число молей в данной массе газа. Для одного моля газа уравнение (2.2.18) имеет вид:

(2.2.19)

.



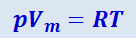к к к