ФИЗИКА

7.15. Элементы физической статистики

Способы описания состояния макроскопической системы. Существует два способа описания состояния коллектива, состоящего из большого числа микрочастиц – термодинамический и статистический. Рассмотрим кратко суть первого и более подробно суть второго.

При термодинамическом подходе коллектив частиц рассматривают как макроскопическую систему, нисколько не интересуясь теми частицами, из которых он состоит. Такую систему называют термодинамической системой.

Термодинамическая система может быть изолированной и неизолированной. Неизолированная система может обмениваться с окружающей средой теплотой и работой.

Состояние системы, в котором она может находиться сколь угодно долго, называется равновесным. Оно однозначно определяется заданием параметров состояния. Основными из них являются объём системы V, давление Р и температура Т.

Совокупность всех видов энергии, заключённой в изолированной системе, называют внутренней энергией (Е) системы. Она складывается из кинетической энергии частиц, образующих систему, потенциальной энергии взаимодействия частиц и внутренней энергии самих частиц (которая не учитывается, так как при тепловых процессах она не изменяется).

Внутренняя энергия является функцией состояния системы. Это означает, что каждому состоянию отвечает только одно значение внутренней энергии независимо от того, каким образом система пришла в это состояние.

Термодинамика базируется на трёх началах, полученных путём обобщения экспериментальных данных. Здесь мы коснёмся только первого из них: изменение внутренней энергии системы dE должно быть равно разности между количеством теплоты ΔQ, полученной системой извне, и работой ΔA, совершённой системой против внешних сил:

(7.15.62)

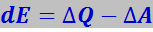
ΔA = pdV, где dV- изменение объёма системы;

ΔQ = Tds, где ds- изменение энтропии.

Подставив эти соотношения в (7.15.62), получим

(7.15.63)

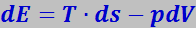
Однако энергия системы может измениться также при изменении числа частиц N в ней, так как каждая уходящая частица уносит с собой определённую энергию. Поэтому в общем виде закон сохранения энергии нужно записать так:

(7.15.64)

где dN - изменение числа частиц в системе.

Параметр μ называется химическим потенциалом системы. Установим его физический смысл. Для изолированной системы постоянного объёма, которая не получает и не отдаёт теплоту, и dV = 0. Тогда

,

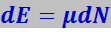а значит,

(7.15.65)

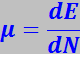
Таким образом, химический потенциал выражает изменение энергии изолированной системы постоянного объёма, вызванное изменением в ней числа на единицу.

Статистический способ описания коллектива. Состояние каждой частицы коллектива описывается заданием трёх её координат и трёх составляющих импульса. Составляя уравнения движения для частиц и решая их, можно, казалось бы, получить полные сведения о поведении системы и предсказать её состояние в любой момент времени.

Однако, если бы такое решение и было проведено (а для 1 м3 воздуха при нормальных условиях пришлось бы решать 1026 связанных между собой уравнений движения молекул), оно оказалось бы бесплодным, так как свойства системы, пришедшей в равновесие, не только не зависят от начальных значений координат и составляющих импульса, но и вообще остаются неизменными с течением времени, несмотря на то, что координаты и импульсы частиц непрерывно изменяются. Отсюда следует, что коллектив, как целое, является системой, качественно отличной от отдельных частиц, и его поведение подчиняется другим закономерностям. Такими закономерностями являются статистические закономерности. Именно им мы обязаны, в частности, тем, что в равных элементах объёма содержится в среднем одинаковое число молекул.

Основной особенностью статистических закономерностей является их вероятностный характер. Они позволяют предсказывать лишь вероятность наступления того или иного события. Так, если бросать монету, то предсказываемая вероятность выпадения герба или решки равна 1/2. От этого значения вероятности могут быть и обязательно будут отступления в отдельных испытаниях. Такие отступления называются флуктуациями. Однако чем больше испытаний, т.е. чем больше членов коллектива, тем определённее и точнее становятся статистические предсказания.

Невырожденные и вырожденные коллективы. Все микрочастицы по характеру поведения в коллективе можно разделить на фермионы и бозоны.

К фермионам относятся электроны, протоны, нейтроны и другие частицы с полуцелым спином: ħ/2, 3ħ/2,... К бозонам относятся фотоны, фононы и другие частицы с целочисленным спином: 0, ħ, 2ħ,...

В коллективе фермионы проявляют в силу принципа Паули стремление к «уединению». Если данное квантовое состояние уже занято, то никакой другой фермион данного типа не может находиться в этом состоянии. Бозоны, напротив, могут неограниченно заселять одно и то же состояние.

Как указанная специфика частиц сказывается на свойствах коллектива? Очевидно, что для проявления специфики микрочастицы должны достаточно часто «встречаться» друг с другом (попадать в одно и то же состояние).

Предположим, что на N одинаковых микрочастиц приходится G различных состояний. Тогда, если

(7.15.66)

то специфика фермионов и бозонов проявиться не может, поскольку в распоряжении каждой микрочастицы имеется множество свободных состояний и вопрос о заселении одного и того же состояния практически не возникает. Подобные коллективы называются невырожденными, а условие (7.15.66) называют условием невырожденности.

Если же выполняется условие

(7.15.67)

то специфика частиц проявляется в полной мере. Такие коллективы могут образовываться, очевидно, только из квантово-механических объектов, так как только у таких объектов параметры состояния изменяются дискретно, вследствие чего число G возможных состояний может быть конечным.

Эти же объекты могут образовывать и невырожденные коллективы, если выполняется условие (7.15.66).

Физическая статистика, изучающая свойства вырожденных коллективов, называется квантовой статистикой.

Наиболее важное различие классической и квантовой статистик связано с принципом тождественности одинаковых частиц. Этот принцип действует только в квантовой механике. Согласно ему, в природе реализуются лишь те квантовые состояния, которые не изменяются при перестановке одинаковых частиц местами. Это приводит к тому, что вероятности микросостояний подсчитываются в классической и квантовой статистиках по-разному, при этом оказывается, что в квантовой статистике системы частиц с целым и полуцелым спинам подчиняются разным статистикам. Квантовая статистика бозонов носит название статистики Бозе-Эйнштейна, а фермионов – статистики Ферми-Дирака.

Функция распределения. Из предыдущего следует: чтобы задать состояние коллектива, например, газа частиц, надо указать его термодинамические параметры; чтобы задать состояние частиц, надо указать значения их координат и составляющих импульсов или энергию частиц, которая определяется их координатами и импульсами.

Связь между этими типами величин осуществляет статистическая функция распределения

(7.15.68)

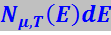
выражающая число частиц с энергией от E до E+ dЕ в системе, состояние которой описывается термодинамическими параметрами μ и Т. Такую функцию называют полной статистической функцией распределения. Для упрощения записи значки термодинамических параметров у функции распределения обычно опускают.

Полную функцию распределения можно представить в виде произведения числа состояний g(E)dE, приходящихся на интервал энергий dE, на вероятность заполнения этих состояний частицами. Обозначим последнюю через f(E). Тогда

(7.15.69)

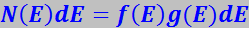
Функцию f(E) называют просто функцией распределения. Её можно также трактовать как среднее число частиц, находящихся в данном состоянии.

Таким образом, задача об отыскании полной функции распределения частиц по состояниям сводится к отысканию функций g(E)dE и f(E). Определим сначала функцию g(E)dE.

к к к