ФИЗИКА

7.13. Динамика электронов в зоне разрешенных значений энергий

Движение свободного электрона под действием электрического поля. Исследование динамики электронов разрешённой зоны начнём с простейшего случая движения свободного электрона под действием электрического поля напряжённости . Это поле действует на электрон с . В соответствии со вторым законом Ньютона он приобретает ускорение . Энергия электрона, который движется со скоростью 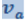(групповая скорость)

(7.13.56)

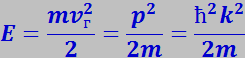
где p – импульс электрона, связанный с волновым числом k соотношением p = ħk.

Графически E(k) выражается параболой. Найдём групповую скорость электрона.

(7.13.57)

Из (7.13.56) найдём , откуда масса электрона:

(7.13.58)

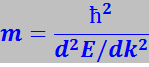
Движение электрона в разрешённой зоне кристалла. Эффективная масса. Рассмотрим теперь движение электрона в зоне разрешённых значений энергии под действием внешнего электрического поля. В этом случае на электрон будут действовать внешняя сила и внутренние силы, которые обусловлены периодическим полем кристалла. По этой причине движение электрона в кристалле будет более сложным, чем движение свободного электрона. Чтобы описывать движение электрона в зоне как свободное движение заряженной частицы, без учёта в уравнениях движения периодического поля кристалла, вводится понятие эффективной массы.

Проиллюстрируем приём введения эффективной массы на следующем примере. Пусть в поле силы тяжести движется тело, помещённое в идеальную, невязкую жидкость. Упрощая сложную картину, возникающую при этом движении, мы можем записать уравнение движения тела массой m0 в виде

(7.13.59)

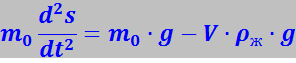
где первый член правой части представляет силу тяжести (s - путь), а второй – силу Архимеда (V – объём тела, ρж - плотность жидкости).

С целью упрощения этого уравнения мы можем исключить из него архимедову силу, приняв, что масса тела m* имеет значение, отличное от m0. Назовём m* эффективной массой. Действительно, уравнение (7.13.59) можно записать в виде

(7.13.60)

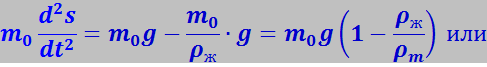
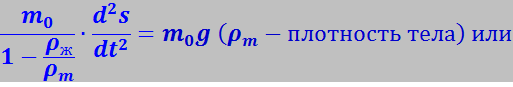
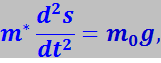
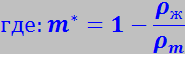
Из (7.13.60) видно, что введённая таким образом эффективная масса m* может отличаться от истинной массы не только по величине, но и по знаку. Действительно, при ρж > ρВ эффективная масса будет отрицательной. Физический смысл этого результата ясен: вследствие того, что подъёмная сила Архимеда, учитываемая эффективной массой m*, превышает в этом случае силу тяжести, направление ускорения тела противоположно направлению единственной силы, фигурирующей в упрощённом уравнении – силы тяжести.

Вернёмся теперь к движению электрона в зоне разрешённых значений энергии. В зависимости E(k) включено уже периодическое поле кристалла. Поэтому эффективную массу электрона можно определить аналогично массе свободного электрона (7.13.58), т.е.

(7.13.61)

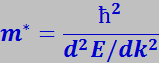
Приписывая электрону эффективную массу, мы можем рассматривать его движение во внешнем поле так, как описывается движение свободного электрона. Однако это движение, как будет показано ниже, не совпадает с движением свободного электрона. Поэтому электрон в твёрдом теле – это квазичастица с отрицательным зарядом и массой, определяемой из (7.13.61). Таким образом, зная зависимость E(k) квазиэлектрона (в дальнейшем будем говорить об электроне для упрощения, понимая, что это квазиэлектрон), можно определить эффективную массу и его динамику под действием внешних воздействий.

Расчёт зависимости E(k) для конкретных кристаллических структур представляет значительные трудности. Отметим некоторые особенности в зависимости E(k), которые характерны для всех кристаллов.

1. В области, близкой к k = 0, кривая зависимости E(k) практически выражается параболой, при k = 0 будет вогнутость.

2. В области, близкой к , кривая будет достигать максимума, так как νc = 0. При будет выпуклость.

3. Между k = 0 и должна быть точка перегиба.

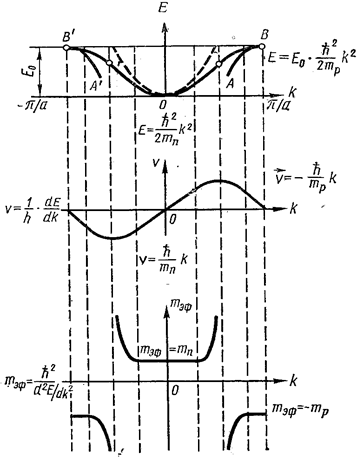
На рис. 7.13.23,а показана зависимость E(k) для электрона в кристаллической структуре. Пунктиром показана зависимость E(k) для свободного электрона. А, А’ – точки перегиба, В, В’ – границы первой зоны Бриллюэна.

Чтобы показать характер изменения эффективной массы m*(k), рассмотрим электрон в первой зоне кристалла при k = 0.

Приложим внешнее поле напряжённостью . На электрон действует сила , которая его ускоряет, и он будет переходить на более высокие энергетические уровни. По мере удаления от начала координат кривая E(k) отходит от параболы и в точке перегиба первая производная достигает экстремума, а вторая производная . На рис. 7.13.23 б изображена групповая скорость электрона ν3(k). Групповая скорость электрона в точке перегиба достигает максимума, а эффективная масса обращается в бесконечность. При переходе через точку перегиба А эффективная масса меняет знак и становится отрицательной. Это означает, что при увеличении k после точки перегиба скорость электрона уменьшается и в точке В ν2 = 0. В точке В электрон испытывает отражение и появляется в точке В’. В интервале от В’ до А’ электрон ускоряется в направлении, противоположном направлению действия силы , и его скорость меняется от 0 до его максимального отрицательного значения, а эффективная масса от -m* до -∞. В точке перегиба А’ знак эффективной массы меняется с отрицательного на положительный и в интервале от А’ до 0 электрон ускоряется в направлении действия силы , скорость при этом увеличивается до нуля, а эффективная масса достигает положительного значения m*. Таким образом, по мере увеличения энергии электрона и перемещения его от дна зоны к её вершине эффективная масса меняется не только по величине, но и по знаку.

к к к