ФИЗИКА

7.12. Зависимость энергии электрона от волнового вектора

Выясним теперь, как зависит энергия Е электронов от их импульса р внутри каждой зоны, т.е. вид кривых E(p). Зависимость E(p) называют законом дисперсии.

Рассмотрим сначала простейший случай движения совершенно свободного электрона вдоль оси Х, описываемого следующим уравнением Шредингера:

(7.12.48)

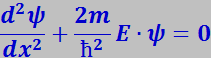
где

(7.12.49)

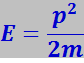
так как свободный электрон обладает только кинетической энергией.

Преобразуем (7.12.49). По формуле де Бройля

(7.12.50)

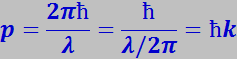
где λ - длина электронной волны, а

(7.12.51)

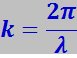
Вектор , по направлению совпадающий с направлением распространения электронной волны, называется волновым вектором электрона. Подставляя (7.12.50) в (7.12.49), получим

(7.12.52)

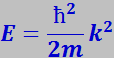
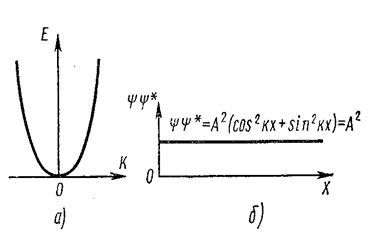
Из (7.12.52) видно, что закон дисперсии для одномерного движения свободного электрона выражается квадратной параболой (рис. 7.12.21).

Решением уравнения (7.12.48) является плоская бегущая волна:

(7.12.53)

где А – амплитуда волны.

Квадрат модуля волновой функции пропорционален вероятности обнаружения электрона в этой или иной области пространства. Из (7.12.53) видно, что для свободного электрона эта вероятность не зависит от координаты электрона, так как ⎪ψ⎪2 = ψψ* = A2. Это означает, что для свободного электрона все точки пространства эквивалентны и вероятность нахождения его в любой из них одинакова (рис. 7.12.21б).

А теперь вернёмся к обсуждению задачи о движении свободного электрона (приближение слабой связи) в периодическом самосогласованном поле, создаваемым кристаллической решёткой. Уравнение Шредингера, учитывающее это поле, имеет вид

(7.12.54)

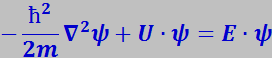
где U – функция, обладающая свойствами

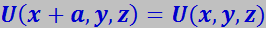
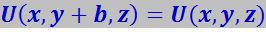
(a,b,c – периоды решётки вдоль осей x,y,z).

Блох доказал, что решение уравнения Шрёдингера с периодическим потенциалом имеет вид

(7.12.55)

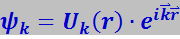
где - функция, имеющая периодичность потенциала, т.е. периодичность решётки.

Решения (7.12.55) называются функциями Блоха.

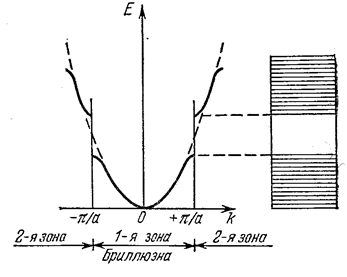
Зависимость E(k) имеет вид, показанный на рис. 7.12.22. Из него видно, что изображённые сплошными линиями зоны квазинепрерывно изменяющейся энергии (разрешённые зоны) чередуются с запрещёнными зонами. При этом каждая зона состоит из близкорасположенных дискретных уровней. Область k-пространства, внутри которой энергия электрона в кристалле изменяется квазинепрерывно, называется зоной Бриллюэна. На границе зон энергия терпит разрыв. Рис. 7.12.22 изображает зоны Бриллюэна в случае одномерного кристалла.

Таким образом, и исходя из приближения сильной связи, и исходя из приближения слабой связи электронов в атомах, мы получили согласующийся результат: энергетический спектр электронов в кристалле должен носить зонный характер.

к к к