ФИЗИКА

7.11. Энергетический спектр электронов в кристалле

Одна из основных задач теории твёрдого тела заключается в определении энергетического спектра электронов в кристалле. Качественное представление об этом спектре можно получить следующим образом. Движение электрона в кристалле можно приближённо описать уравнением Шредингера:

(7.11.46)

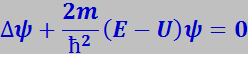
где U – потенциальная,

Е – полная энергия электрона,

т – его масса.

Если обобществлённые электроны сохраняют достаточно сильную связь с атомами, то их потенциальную энергию можно представить в виде

(7.11.47)

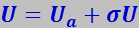
где Ua - потенциальная энергия электрона в изолированном атоме.

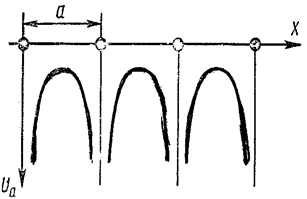
Для кристалла она является периодической функцией с периодом, равным параметру решётки, так как энергия электрона повторяется при переходе его от одного атома к другому (рис. 7.11.18); σU представляет собой поправочный член, учитывающий влияние соседних атомов на эту энергию.

Если в (7.11.47) пренебречь поправочным членом σU, т.е. рассматривать так называемое нулевое приближение, то в качестве волновой функции и энергии электрона в кристалле следует взять волновую функцию ψa и энергию Ea(n,ℓ) электрона в изолированном атоме: ψ = ψa, E = Ea (n,ℓ), где n,ℓ - главное и орбитальное квантовые числа, определяющие энергию электрона в атоме.

Различие между кристаллом и отдельным атомом состоит в этом случае в следующем. В то время как в изолированном атоме данный энергетический уровень Ea (n,ℓ) является единственным, в кристалле, состоящем из N атомов, он повторяется N раз. Иначе говоря, каждый уровень в кристалле оказывается N-кратно вырожденным. Такое вырождение называется перестановочным.

Учтём теперь поправочный член σU в потенциальной энергии. По мере сближения изолированных атомов и образования из них решётки каждый атом попадает во всё возрастающее поле своих соседей, с которыми он взаимодействует. Это поле приводит к снятию вырождения, в том числе и перестановочного. Поэтому каждый энергетический уровень, не вырожденный в изолированном атоме, расщепляется на N близко расположенных друг от друга подуровней, образующих энергетическую зону.

Если энергетический уровень имел в атоме (2ℓ+1)-кратное вырождение, то соответствующая ему энергетическая зона будет состоять из N(2ℓ+1) подуровней. Так, уровень s даёт зону S, состоящую из N подуровней и способную вместить 2N электронов; уровень р даёт зону Р, состоящую из 3N подуровней и способную вместить 6N электронов и т.д.

Расстояние между подуровнями в зоне кристалла обычных размеров очень мало. В кристалле размером 1 см3 содержится 1022 атомов. При ширине зоны порядка 1 эВ расстояние между подуровнями в ней равно примерно 10-22 эВ. Это расстояние столь ничтожно, что зоны можно считать практически непрерывными. Однако тот факт, что число уровней в зоне является всё-таки конечным, играет важную роль в определении характера распределения электронов по состояниям.

Наибольшее влияние поле решётки оказывает на внешние валентные электроны атомов. Поэтому состояние этих электронов в кристалле претерпевает наибольшее изменение, а энергетические зоны, образованные из энергетических уровней этих электронов, оказываются наиболее широкими.

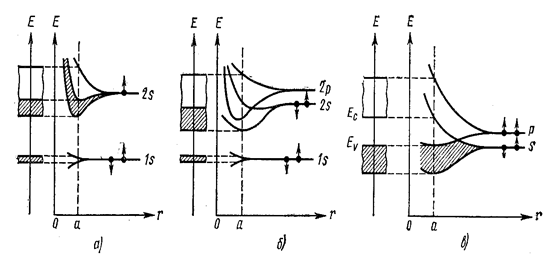
Внутренние же электроны, сильно связанные с ядром, испытывают лишь незначительное возмущение от соседних атомов, вследствие чего их энергетические уровни в кристалле остаются практически столь же узкими, как и в изолированных атомах. На рис. 7.11.19 показана схематическая картина образования энергетических зон в кристалле из дискретных атомных уровней.

Таким образом, каждому энергетическому уровню изолированного атома в кристалле соответствует зона разрешённых энергий. Эти зоны разделены областями запрещённых энергий – запрещёнными зонами Eg. С увеличением энергии электрона в атоме ширина разрешённых зон увеличивается, ширина запрещённых – уменьшается.

В качестве примера на рис. 7.11.20 приведены энергетические зоны лития и химических элементов, имеющих структуру алмаза (алмаз, кремний, германий). В кристалле лития (рис. 7.11.20а) уровень 1s расщеплён слабо, уровень 2s - сильнее. У элементов типа алмаза зоны, возникающие из уровней s и р, перекрываясь, разделяются на две зоны так, что в каждой из них содержится по четыре состояния на атом: одно s-состояние и три р-состояния. Эти зоны разделены запрещённой зоной. Нижнюю разрешённую зону называют валентной, верхнюю – зоной проводимости.

к к к