ФИЗИКА

7.7. Классическая теория электропроводности металлов

Она была создана Друде исходя из представлений о свободных электронах, а затем усовершенствована Лоренцем. Друде предположил, что электроны проводимости в металле ведут себя подобно молекулам идеального газа. В промежутках между соударениями они движутся совершенно свободно, пробегая в среднем некоторый путь 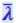. При этом, в отличие от молекул, электроны сталкиваются преимущественно не между собой, а с ионами, образующими кристаллическую решётку. Эти столкновения приводят к установлению теплового равновесия между электронным газом и кристаллической решёткой.

Полагая, что на электронный газ могут быть распространены результаты кинетической теории газов, оценим величину средней скорости (ν) электронов при T = 300K:

При включении поля на хаотическое тепловое движение со скоростью (ν) накладывается упорядочное движение электронов с некоторой средней скоростью (u). Величину (u) можно оценить, исходя из формулы

(7.7.33)

где j - плотность тока.

Для медных проводов 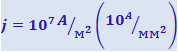. Тогда:

.

Таким образом, (u)<<(ν). Поэтому при вычислениях модуль результирующей скорости можно заменять модулем скорости теплового движения .

Закон Ома. Друде считал, что при соударении с ионом кристаллической решётки приобретённая электроном дополнительная энергия передаётся иону, а значит, скорость u делается равной нулю.

Предположим, что поле, ускоряющее электроны, однородно. Тогда под действием поля электрон получит ускорение , и к концу пробега скорость упрядочного движения достигает в среднем значения

(7.7.34)

где τ - среднее время между двумя последовательными соударениями электрона с ионами решётки.

Друде не учитывал распределение электронов по скоростям и приписывал всем электронам одинаковое значение скорости v. В этом приближении

(7.7.35)

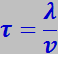
Подставив (7.7.35) в (7.7.34), получим

.

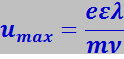Скорость U изменяется за время пробега линейно. Поэтому её среднее за пробег значение равно половине максимального

(7.7.36)

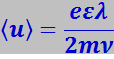
Подстановка этого выражения в (7.7.33) даёт

(7.7.37)

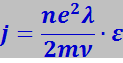
Мы получили закон Ома в дифференциальной форме

(7.7.38)

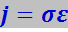
где проводимость .

Если бы электроны не сталкивались с ионами решётки, длина свободного пробега λ, а следовательно, и проводимость были бы бесконечно велики. Таким образом, согласно классическим представлениям электрическое сопротивление металлов обусловлено соударениями свободных электронов с ионами кристаллической решётки.

Закон Джоуля-Ленца. К концу свободного пробега электрон приобретает дополнительную кинетическую энергию, среднее значение которой равно

(7.7.39)

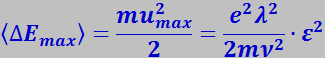
При столкновении с ионом электрон полностью передаёт приобретённую энергию решётке. Сообщённая решётке энергия идёт на увеличение внутренней энергии металла, проявляющейся в его нагревании.

Каждый электрон претерпевает за секунду в среднем соударений, сообщая всякий раз решётке энергию (7.7.39). Поэтому в единице объёма за единицу времени должно выделяться тепло

(7.7.40)

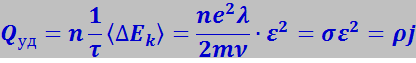
где n – число электронов проводимости в единице объёма,

- удельное сопротивление;

Qуд - удельная тепловая мощность тока.

Соотношение (7.7.40) выражает закон Джоуля-Ленца в дифференциальной форме.

Закон Видемана-Франца. Из опыта известно, что наряду с высокой электропроводностью металлы отличаются также большой теплопроводностью. Видеман и Франц установили эмпирический закон, согласно которому отношение коэффициента теплопроводности χ к коэффициенту электропроводности σ для всех металлов приблизительно одинаково и изменяется пропорционально температуре.

Из классической теории следует:

(7.7.41)

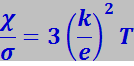
Подстановка в (7.7.41) числовых значений k и е даёт выражение

,

которое хорошо согласуется с экспериментальными данными.

Однако, когда Лоренц уточнил расчёты, отношение стало хуже сходится с экспериментом.

Итак, классическая теория смогла объяснить законы Ома и Джоуля-Ленца, а также дала качественное объяснение закона Видемана-Франца.

Вместе с тем эта теория встретилась с существенными трудностями. Из них основными являются следующие.

Из формулы вытекает, что сопротивление металлов должно возрастать пропорционально квадратному корню из температуры, так как из всех входящих в это соотношение параметров только , остальные же параметры от температуры не зависят. Этот вывод теории противоречит опытным данным, согласно которым сопротивление металлов растёт пропорционально первой степени Т.

Далее, для того, чтобы получить закон Ома, пришлось предположить, что электрон при своём движении сталкивается со всеми попадающимися ему на пути узлами кристаллической решётки, а чтобы получить экспериментальное значение удельного сопротивления, приходиться предполагать, что электрон без столкновений может проходить тысячи межузельных расстояний.

Наконец, теплоёмкость металлов должна быть в 1,5 раза больше теплоёмкости диэлектриков, так как электронный газ должен вносить свой вклад в теплоёмкость. В действительности же теплоёмкость металлов не отличается заметно от теплоёмкости диэлектриков. Объяснить эти и другие несоответствия смогла лишь квантовая теория.

к к к