‘»«» ј
2.2.2. Основное уравнение молекулярно-кинетической теории идеальных газов
Одно из основных свойств газа – оказывать давление на стенки содержащего его сосуда. Именно своим давлением газ чаще всего и обнаруживает своё присутствие. Оно определяется силами, возникающими при столкновении молекул со стенками.
Мы не знаем величины сил взаимодействия молекулы и стенки и поэтому не можем вычислить силу, испытываемую стенкой при соударении с нею одной молекулы. Но нетрудно вычислить среднюю силу, возникающую при соударении со стенкой многих молекул, если известны их скорости и, если предположить, что соударения являются упругими. В этом случае сила равна и противоположна по знаку изменению импульса молекул, соударяющихся со стенкой в единицу времени (второй закон Ньютона).
Пусть некоторая молекула движется в сосуде со скоростью 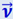 . Как бы ни была направлена эта скорость, её всегда можно разложить на три составляющие, из которых одна перпендикулярна стенке сосуда, а две других – параллельны ей. Нас, разумеется, интересует только первая из них, так как при ударе только она и может измениться (рис. 2.2.1).
. Как бы ни была направлена эта скорость, её всегда можно разложить на три составляющие, из которых одна перпендикулярна стенке сосуда, а две других – параллельны ей. Нас, разумеется, интересует только первая из них, так как при ударе только она и может измениться (рис. 2.2.1).
|
Если перпендикулярная к стенке составляющая скорости равна u, то соответствующая составляющая импульса молекулы равна mu, где m - масса молекулы.
После соударения со стенкой молекула изменит направление составляющей скорости u на обратное, но численное значение её при этом не изменится. Импульс молекулы теперь станет равным -mu. Значит изменение импульса молекулы при соударении равно -2mu.
Пусть теперь на некоторую площадку ΔS стенки в единицу времени попадает N молекул, составляющие скорости которых, перпендикулярные ΔS, равны u. Тогда общее изменение импульса всех этих молекул в единицу времени равно -2muN и равно взятой с обратным знаком величине силы, действующей на площадку, т.е.
(2.2.1)
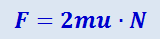 .
.
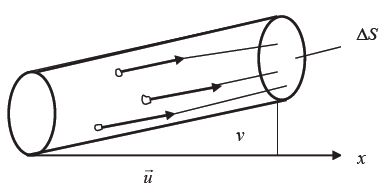
Остаётся вычислить число молекул N, попадающих в единицу времени на площадку ΔS. В единицу времени до стенки дойдут только те молекулы, которые находятся не далее, чем на расстоянии ν от неё, т.е. те молекулы, которые заключены в объёме цилиндра с площадью основания ΔS и образующей ν. Объём такого цилиндра равен, очевидно, u⋅ΔS (рис. 2.2.2).
Рис. 2.2.2 |
Если в единице объёма газа содержится n молекул, то число их в объёме u⋅ΔS равно n⋅u⋅ΔS. Из них только половина попадает на площадку ΔS. Остальные в силу полной беспорядочности молекулярных движений движутся не к стенке, а от неё. Значит, в единицу времени ударяется о площадку ΔS
(2.2.2)
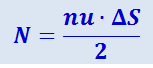
молекул. Сила же, испытываемая площадкой ΔS от ударов всех N молекул, согласно с (2.2.1), равна
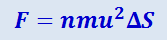 .
.
Значит давление на стенку равно:
(2.2.3)
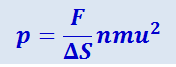 .
.
Таково было бы давление газа, если бы все молекулы имели одинаковые составляющие скорости в направлении, перпендикулярном стенке.
В действительности же молекулы могут иметь различные скорости, как по величине, так и по направлению. Вычислим давление газа в этих условиях.
Пусть в некотором объёме газа V содержится N молекул одинаковой массы m с плотностью 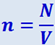 .
.
Пусть из числа n молекул, содержащихся в единице объёма, n1 молекул имеют скорость ν1, у n1 молекул скорость равна ν2 и т.д., так что
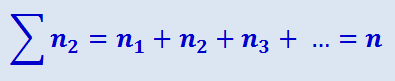 .
.
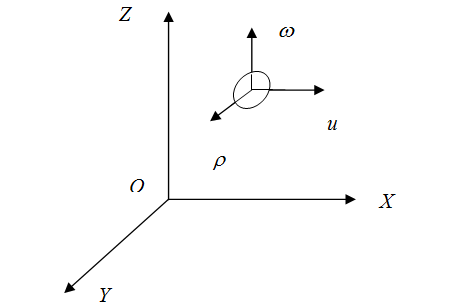
Обозначим составляющие этих скоростей по осям координат X,Y,Z через u1, ρ1, ω1; u2, ρ2, ω2 и т.д. Вычислим давление газа на какую-нибудь площадку ΔS, перпендикулярную, например, оси Х (рис. 2.2.3), т.е. величину px. Это давление px будет равно сумме давлений, испытываемых площадкой со стороны каждой из указанных групп молекул:
(2.2.4)
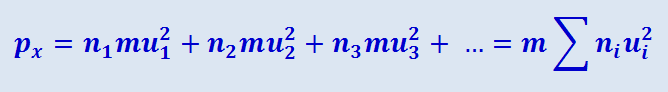 .
.
Рис. 2.2.3 |
Точно так же давление на любую площадку, перпендикулярную осям Y и Z, определяется равенствами:
(2.2.5)
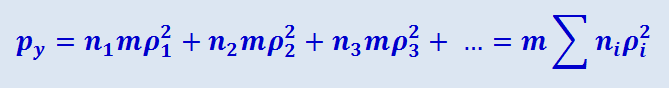 ,
,
(2.2.6)
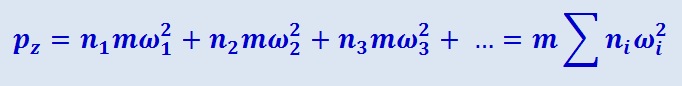 .
.
Ввиду полной хаотичности движений молекул давление газа в любом направлении должно быть одним и тем же, т.е.
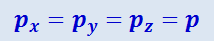 .
.
Это закон Паскаля, который как раз и является следствием хаотичности молекулярных движений.
Сложим почленно уравнения (2.2.4), (2.2.5), (2.2.6):
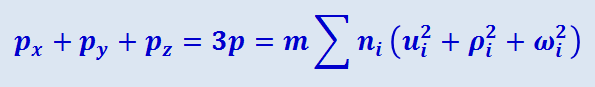 .
.
Так как
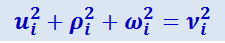 ,
,
то
(2.2.7)
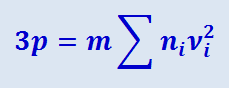 .
.
Величина ∑niνi2 - это сумма квадратов скоростей всех молекул в единице объёма газа. При большом числе молекул нет нужды знать значение квадрата скорости каждой молекулы. Важно знать среднее значение этой величины, т.е. 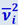 .
.
По определению
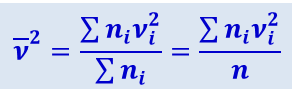 .
.
Отсюда следует, что
(2.2.8)
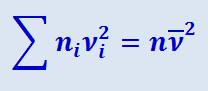 .
.
Подставив (2.2.8) в (2.2.7), получим:
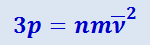 ,
,
или
(2.2.9)
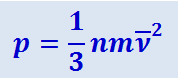 ,
,
или
(2.2.10)
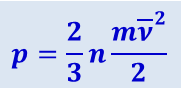 .
.
Величина 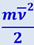 представляет собой среднюю кинетическую энергию одной молекулы газа. Давление идеального газа равно двум третям средней кинетической энергии молекул единицы объёма газа. Это один из важнейших выводов кинетической теории газов. Формула (2.2.10) устанавливает связь между молекулярными величинами (масса и скорость молекул) и величиной давления, характеризующей газ как целое и непосредственно измеряемой на опыте. Уравнение (2.2.10) часто называют основным уравнением кинетической теории газов.
представляет собой среднюю кинетическую энергию одной молекулы газа. Давление идеального газа равно двум третям средней кинетической энергии молекул единицы объёма газа. Это один из важнейших выводов кинетической теории газов. Формула (2.2.10) устанавливает связь между молекулярными величинами (масса и скорость молекул) и величиной давления, характеризующей газ как целое и непосредственно измеряемой на опыте. Уравнение (2.2.10) часто называют основным уравнением кинетической теории газов.
Важно подчеркнуть, что давление газа определяется средней кинетической энергией его молекул. Это значит, что давление газа – величина органически связанная с тем, что газ состоит из большого числа молекул. Не имеет, поэтому смысла говорить, например, о давлении, создаваемом одной или немногими молекулами. О таких понятиях, которые имеют смысл только для систем, содержащих очень много частиц, говорят, что они имеют статистический характер.
Температура. Из (2.2.10) видно, что давление идеального газа зависит от его плотности n и от средней энергии поступательного движения молекулы (молекула – точка может совершать только поступательное движение). Можно показать, что обе эти величины не зависят друг от друга.
Если привести в соприкосновение два газа с различными значениями средней кинетической энергии молекул, то через некоторое время значения средних кинетических энергий молекул обоих газов станут одинаковыми. Это выравнивание произойдёт благодаря тому, что молекулы обоих газов, сталкиваясь друг с другом (ведь молекулы на самом деле не являются точками и поэтому сталкивания между ними неизбежны), обмениваются энергией.
При этом имеет место переход энергии от газа с более высоким значением средней энергии к газу более низким значением этой величины. После выравнивания энергии в обоих газах наступит состояние так называемого теплового равновесия, при котором переход энергии от одного газа к другому прекращается, хотя столкновения хаотически движущихся частиц и будут продолжаться.
Из повседневного опыта известно, что совершенно таким же образом ведут себя два тела, неодинаково нагретые, т.е. имеющие различную температуру. При соприкосновении таких тел тоже происходит передача энергии от одного тела к другому до тех пор, пока их температуры не выравниваются.
Естественно поэтому считать, что средняя кинетическая энергия молекул, определяющая при данной плотности идеального газа его давление, является в то же время и мерой температуры. Это тем более оправданно, что средняя кинетическая энергия молекул идеального газа не зависит от плотности газа. Поэтому можно считать, что она связана только с температурой.
В применении к идеальному газу удобно считать, что температура газа равна двум третям средней кинетической энергии одной молекулы. Обозначив температуру через  , можно написать
, можно написать
(2.2.11)
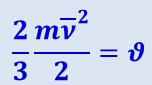 .
.
При таком определении температуры она должна, очевидно, измеряться в единицах энергии. Однако практически пользоваться такой единицей температуры неудобно, потому что непосредственное измерение кинетической энергии молекулы затруднительно.
По этой причине, а также потому, что величиной температуры пользовались ещё до того, как были развиты молекулярно-кинетические представления и для температуры уже давно выбрана единица измерения – градус, принято пользоваться именно этой единицей, несмотря на её условность.
В технике и в быту используется температура, отсчитанная по шкале Цельсия. Единица этой шкалы называется градусом Цельсия (°C). В физике пользуются термодинамической температурой. Единица термодинамической температуры – кельвин (К). Числовые значения кельвина и градуса Цельсия одинаковы. Термодинамическая температура Т связана температурой t по шкале Цельсия соотношением
(2.2.12)
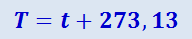 .
.
Температура, равная 0 K, называется абсолютным нулём температуры; ему соответствует t = -273,15°C. Температуре t = 0°C соответствует T = 273,15 K.
Если измерять температуру в градусах, то необходимо ввести коэффициент, переводящий энергетические характеристики в градусы. Обозначив этот переводной множитель через k и подставив в (2.2.11), получим:
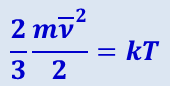 ,
,
где Т – температура, измеренная в градусах, или
(2.2.13)
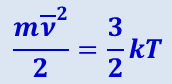 .
.
Формула (2.2.13) относится к молекуле, которую мы условились считать подобной точке. Её кинетическая энергия – это кинетическая энергия поступательного движения, скорость которого может быть разложена на три составляющих. Если учесть, что вследствие хаотичности движения молекул энергия равномерно распределяется по всем трём составляющим движения, то на каждую из них приходится энергия  .
.
Множитель k называется постоянной Больцмана. В системе СИ
 .
.
Имеется в виду градус Цельсия.
Из формулы (2.2.13) видно, что температура, так же, как и давление, определяется средней кинетической энергией молекулы идеального газа. Поэтому температура, как и давление, относится к числу статистических величин. Нельзя говорить о «температуре» одной или немногих молекул, о «горячих» и «холодных» молекулах. Не имеет смысла говорить о температуре газа в космическом пространстве, где число молекул настолько мало, что они не образуют газа в обычном смысле слова.
к к к