ФИЗИКА

7.5. Теплоемкость твердого тела

Тепловая энергия твёрдого тела Eреш складывается из энергии нормальных колебаний решётки. Число нормальных колебаний, приходящихся на спектральный участок dω, равно g(ω)dω (7.4.15). Умножая это число на среднюю энергию нормального колебания (7.4.24), получим суммарную энергию нормальных колебаний, заключённых в интервале dω:

.

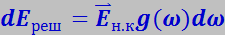Проинтегрировав это выражение по всему спектру нормальных колебаний, т.е. в пределах от 0 до ωД, получим энергию тепловых колебаний решётки твёрдого тела:

(7.5.25)

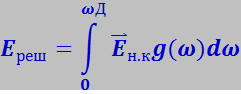
Теплоёмкость CV твёрдого тела при постоянном объёме выражает изменение тепловой энергии при изменении температуры тела на 1°C и находится дифференцированием Eреш по Т:

(7.5.26)

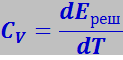
Ограничимся качественным рассмотрением зависимости CV(T) для двух областей температур: для области температур Т, значительно меньших температуры Дебая Θ,  T<<Θ, которую называют областью низких температур, и для области температур выше температуры Дебая T>Θ, которую называют областью высоких температур.

Область низких температур. В этой области возбуждаются в основном низкочастотные нормальные колебания, кванты энергии которых ħω<kT. В этом случае приближённое значение средней энергии нормальных колебаний можно определить, разлагая экспоненту в ряд и ограничиваясь вторым членом разложения. Тогда получим

.

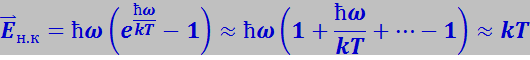Следовательно, в области низких температур средняя энергия каждого нормального колебания растёт пропорционально абсолютной температуре Т :

(7.5.27)

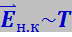
Этот рост обусловлен тем, что с повышением температуры происходит увеличение степени возбуждения нормального колебания, которое и приводит к росту его средней энергии.

Помимо этого в области низких температур повышение температуры вызывает возбуждение новых нормальных колебаний с более высокими частотами. Приближённое значение их z можно вычислить, используя (7.4.15). Считая, что при температуре Т возбуждаются все нормальные колебания вплоть до частоты , найдём

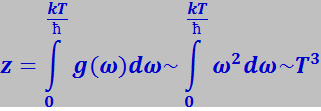
Как видно с повышением температуры число возбуждённых нормальных колебаний растёт пропорционально кубу абсолютной температуры Т:

(7.5.28)

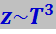
Таким образом, в области низких температур энергия кристалла с повышением температуры увеличивается вследствие действия двух механизмов:

1) роста средней энергии каждого нормального колебания из-за повышения степени его возбуждения;

2) роста числа возбуждённых нормальных колебаний решётки.

Первый механизм вызывает рост энергии, пропорциональный Т, второй – пропорциональный Т3.

Поэтому в целом с повышением температуры энергия растёт пропорционально Т4:

(7.5.29)

а теплоёмкость – пропорционально T3:

(7.5.30)

Соотношение (7.5.30) выражает закон Дебая, хорошо выполняющийся в области низких температур.

Область высоких температур. При температуре Дебая возбуждаются все нормальные колебания решётки, и дальнейшее повышение температуры не может привести к увеличению их числа. Поэтому в области высоких температур изменение энергии твёрдого тела может происходить только за счёт повышения степени возбуждения нормальных колебаний, приводящего к увеличению их средней энергии . Так как , то и изменение энергии тела в целом с ростом температуры должно происходить пропорционально Т:

(7.5.31)

а теплоёмкость не должна зависеть от Т:

(7.5.32)

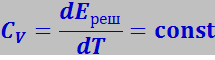
Соотношение (7.5.32) выражает закон Дюлонга и Пти, хорошо оправдывающийся на опыте.

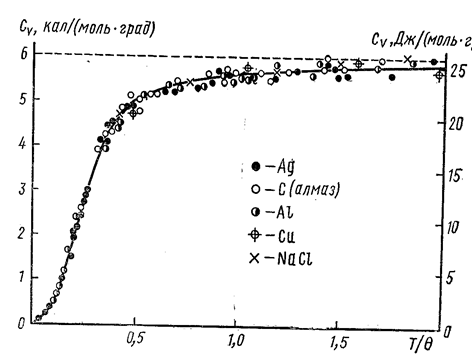
Между областями низких и высоких температур лежит достаточно широкая область так называемых средних температур, в которой происходит постепенный переход от закона Дебая к закону Дюлонга и Пти. Это наиболее сложная для расчёта область температур. График зависимости CV(T) представлен на рис. 7.5.13. Теплоёмкость электронного газа будет рассмотрена ниже.

к к к