ФИЗИКА

7.4. Спектр нормальных колебений решетки

Сначала рассмотрим простейший случай нормальных колебаний линейной цепочки атомов (рис. 7.3.10).

Длины волн, которые могут возникать в такой цепочке, равны

(7.4.12)

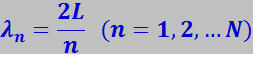
где L – длина цепочки;

N – число атомов в ней.

Очевидно, что число нормальных колебаний z, которые могут возникать в ней с длиной волны, равной или большей λn, равно n:

.

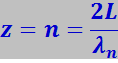Аналогично число стоячих волн в трёхмерном кристалле (например, в кубе с ребром L и объёмом V = L3), обладающих длиной, равной или большей λ, должно быть равно

.

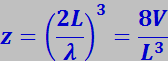Более строгий расчёт даёт

(7.4.13)

.

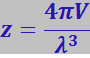Так как (где v – скорость распространения волн (звука) в цепочке), то

(7.4.14)

Дифференцируя это выражение, получим

(7.4.15)

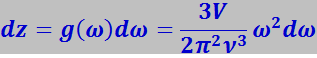
Формула (7.4.15) выражает число нормальных колебаний, заключённое в интервале частот от ω до ω + dω. Функция

(7.4.16)

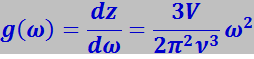
определяет плотность заполнения спектрального участка dω нормальными колебаниями, а следовательно, и частотный спектр этих колебаний.

Функция gω называется функцией распределения нормальных колебаний по частотам.

Так как общее число нормальных колебаний, которое может возникнуть в решётке, равно 3N, то gω должно удовлетворять следующему условию нормировки:

(7.4.17)

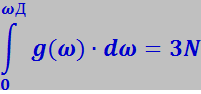
где ωД - максимальная частота, ограничивающая спектр нормальных колебаний сверху.

Подставив (7.4.16) в (7.4.17) и проинтегрировав, получим

(7.4.18)

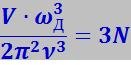
Отсюда находим

(7.4.19)

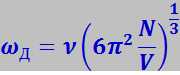
Частота ωД называется характеристической дебаевской частотой.

Температура

(7.4.20)

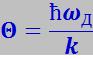
(k – постоянная Больцмана) называется характеристической температурой Дебая.

При ней в твёрдом теле возбуждается весь спектр нормальных колебаний, включая и колебание с максимальной частотой ωД. Поэтому дальнейшее повышение температуры (выше Θ) не может вызывать появление новых нормальных колебаний. Действие температуры в этом случае сводится лишь к увеличению степени возбуждения каждого нормального колебания, приводящего к возрастанию их средней энергии.

Понятие о фононах. Можно показать, что энергия нормального колебания решётки равна энергии осциллятора, имеющего массу, равную массе колеблющихся атомов, и колеблющегося с частотой, равной частоте нормального колебания. Такие осцилляторы называются нормальными. Тогда полная энергия кристалла Eреш, в котором возбуждены все 3N нормальных колебаний, равна

,

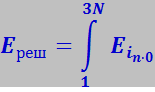где Ein⋅o - энергия i-го нормального осциллятора, и задача об определении средней энергии кристалла сводится к более простой задаче об определении средней энергии нормальных осцилляторов.

Напомним: энергия квантового осциллятора определяется соотношением:

(7.4.21)

где ω - частота колебаний осциллятора,

n – квантовое число.

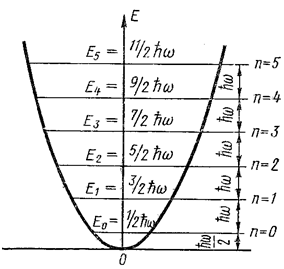
На рис. 7.4.11 показан энергетический спектр линейного гармонического осциллятора. Он состоит из совокупности дискретных уровней, отстоящих друг от друга на расстоянии, равном ħω.

Так как энергия нормального колебания Eн.к. = Ен.о., то энергия нормальных колебаний решётки должна определяться выражением (21), а их энергетический спектр должен совпадать со спектром, показанным на рис. 7.4.11.

Минимальная порция энергии, которую может поглотить или испустить решётка при тепловых колебаниях, соответствует переходу возбуждаемого нормального колебания с данного энергетического уровня на близлежащий соседний уровень и равна

(7.4.22)

.

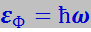Эту порцию, или квант энергии, тепловых колебаний решётки называют фононом.

Для пояснения приведём следующую аналогию. Полость абсолютно чёрного тела заполнена равновесным тепловым излучением. С квантовой точки зрения это излучение трактуется как газ, образованный квантами света – фотонами.

Точно так же поле упругих волн, заполняющих кристалл, можно трактовать как газ, образованный квантами нормальных колебаний решётки – фононами, обладающими энергией εФ = ħω и импульсом p=ħk (k = 2π/λ - волновое число).

Отсюда, нагретый кристалл можно уподобить ящику, заполненному фононным газом.

Фонон во многих отношениях ведёт себя так, как если бы он был частицей. Однако в отличие от обычных частиц фонон не может возникнуть в вакууме – для своего возникновения и существования фонон нуждается в некоторой среде. Таким образом, фонон является квазичастицей.

Фононы описываются функцией распределения Бозе-Эйнштейна

(7.4.23)

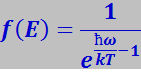
которая выражает среднее число фононов, обладающих энергией εФ = ħω.

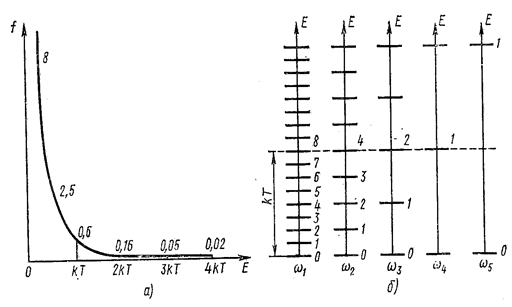
График функции представлен на рис.7.4.12а.

В зависимости от степени возбуждения нормального колебания оно может «испускать» то или иное число одинаковых фононов. Так, при данной температуре Т в решётке возбуждаются все нормальные колебания вплоть до колебаний с энергией ħω ≈ kT; колебания с более высокими частотами, которым отвечают кванты энергий ħω > kT, практически почти не возбуждаются. Это наглядно видно из рис. 7.4.12б. Горизонтальными чёрточками здесь изображены энергетические спектры нормальных колебаний, имеющие частоты ; пунктиром показан уровень, отвечающий энергии kT. Из рис. 7.4.12б следует, что при данной температуре Т колебание с частотой ω, возбуждено примерно до 4-го уровня. Это означает, что такое нормальное колебание «порождает» в среднем четыре одинаковых фонона с энергией каждый. Нормальное колебание с частотой ω2 возбуждено примерно до 2-го уровня; с частотой ω3 = kT - до 1-го уровня; колебание же с частотой ω4 требует для своего возбуждения столь высокой энергии ħω4, что при температуре Т оно возбуждается лишь очень слабо. Ещё слабее возбуждаются более высокие частоты. Поэтому приближённо можно считать, что при данной температуре T < Θ в твёрдом теле возбуждаются нормальные колебания вплоть до частоты ω, которой соответствует энергия ħω ≈ kT.

Как отмечено выше, функция распределения f(E) выражает среднее число фононов, обладающих энергией εФ = ħω. Поэтому, умножая (7.4.23) на ħω, получим среднюю энергию возбуждённого нормального колебания, имеющего частоту ω:

(7.4.24)

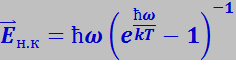
к к к