ФИЗИКА

7.3. Классическая и квантовые теории теплоемкости твердых тел

Начнём с классических представлений, согласно которым кристалл, состоящий из N атомов, является системой с 3N колебательными степенями свободы, на каждую из которых приходится в среднем энергия kT (1/2kT в виде кинетической и 1/2kT в виде потенциальной энергии). Из этих представлений вытекает установленный экспериментально закон Дюлонга и Пти, который утверждает, что молярная теплоёмкость CV всех химических простых тел в кристаллическом состоянии одинакова и равна 3R. Действительно, внутренняя энергия одного моля кристалла U равна

,

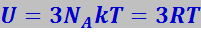где NA = 6,022 ⋅ 1023 моль-1 - число Авогадро;

k = 1,38 ⋅ 10-23 Дж/К - постоянная Больцмана;

R = 8,31 Дж/моль⋅К.

Тогда

(7.3.7)

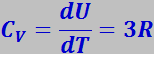
Закон Дюлонга и Пти выполняется достаточно хорошо только при сравнительно высоких температурах. При низких температурах теплоёмкость кристаллов убывает, стремясь к нулю при приближении к 0°К.

Такой ход кривой CV(T) классическая физика объяснить не смогла.

Качественно ход кривой теплоёмкости при низких температурах удалось получить Эйнштейну. Он отождествил кристаллическую решётку из N атомов с системой 3N независимых гармонических осцилляторов, колеблющихся с одинаковой собственной частотой ω и предположил, что энергия осцилляторов En меняется дискретно. Как известно в настоящее время, .

Приняв, что распределение осцилляторов по состояниям с различной энергией подчиняется закону Больцмана, для средней энергии осциллятора <E> получим выражение

(7.3.8)

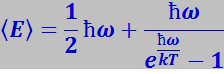
Существование нулевой энергии во времена Эйнштейна было неизвестно. Поэтому первое слагаемое в (7.3.8) у Эйнштейна отсутствовало.

Умножив второе слагаемое выражения (7.3.8) на 3N, Эйнштейн получил для внутренней энергии кристалла формулу

(7.3.9)

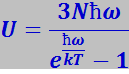
Продифференцировав (7.3.9) по температуре, Эйнштейн нашёл теплоёмкость кристалла:

(7.3.10)

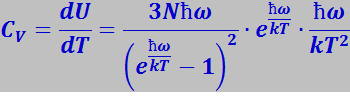
Рассмотрим два предельных случая:

1. Высокие температуры (kT>>ħω). В этом случае можно положить в знаменателе и - в числителе формулы (7.3.10).

Тогда CV = 3Nk. Таким образом, мы пришли к закону Дюлонга и Пти.

2. Низкие температуры (kT<<ħω). В этом случае единицей в знаменателе (7.3.10) можно пренебречь. Тогда

(7.3.11)

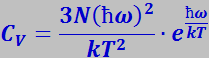
Экспоненциальный множитель изменяется значительно быстрее, чем T2. Поэтому при приближении к абсолютному нулю выражение (7.3.11) будет стремиться к нулю практически по экспоненциальному закону. Опыт показывает, что теплоёмкость кристаллов вблизи абсолютного нуля изменяется не экспоненциально, а по закону T3. Количественного согласия с опытом удалось достичь Дебаю.

Дебай учёл, что колебания атомов в кристаллической решётке не являются независимыми. Смещение одного из атомов из положения равновесия влечёт за собой смещение других соседних с ним атомов, и в кристалле возбуждается коллективное движение в форме упругой волны, охватывающей все частицы кристалла. Такое коллективное движение называется нормальным колебанием решётки. Число нормальных колебаний, которое может возникнуть в решётке, равно числу степеней свободы частиц кристалла, т.е. 3N (N – число частиц, образующих кристалл).

Проиллюстрируем сказанное на одномерной модели твёрдого тела – линейной цепочки атомов, отстоящих друг от друга на расстоянии а и способных колебаться в направлении, перпендикулярном длине цепочки (рис. 7.3.10). Такую цепочку можно трактовать как струну.

Если концы цепочки закреплены, то основное колебание, отвечающее самой низкой частоте, соответствует возникновению стоячей волны с узлами на концах (рис. 7.3.10б, кривая 1). Следующему колебанию отвечает стоячая волна с узлами не только на концах, но и на середине цепочки (кривая 2). Третьему колебанию, или, как говорят, третьей гармонике соответствует стоячая волна с двумя узлами, делящая цепочку на три равные части (кривая 3), и т.д. Очевидно, что самая короткая длина волны, которая может образоваться в такой цепочке, равна удвоенному расстоянию между атомами цепочки (рис. 7.3.10в): λmin = 2a.

к к к