ФИЗИКА

5.4.3. Поляризация света при двойном луче преломлении

При прохождении света через все прозрачные кристаллы, за исключением принадлежащих к кубической системе, наблюдается явление, заключающееся в том, что упавший на кристалл луч разделяется на два луча, распространяющихся с разными скоростями и в разных направлениях. Это явление получило название двойного лучепреломления.

Кристаллы, обладающие двойным лучепреломлением, подразделяются на одноосные и двуосные. У одноосных кристаллов один из преломлённых лучей подчиняется обычному закону преломления. Этот луч называется обыкновенным и обозначается буквой о. Для другого луча, называемого необыкновенным (его обозначают буквой е), отношение синуса угла падения и угла преломления не остаётся постоянным при изменении угла падения. Даже при нормальном падении света на кристалл необыкновенный луч не лежит, как правило, в одной плоскости с падающим лучом и нормально к преломляющей поверхности. Примерами одноосных кристаллов могут служить исландский шпат, кварц и турмалин. У двуосных кристаллов (слюда, гипс) оба луча необыкновенные. Дальше мы ограничимся рассмотрением только одноосных кристаллов.

У одноосных кристаллов имеется направление, вдоль которого обыкновенный и необыкновенный лучи распространяются, не разделяясь, и с одинаковой скоростью. Это направление называется оптической осью кристалла. Любая прямая, параллельная данному направлению, также является оптической осью кристалла.

Любая плоскость, проходящая через оптическую ось, называется главным сечением, или главной плоскостью, кристалла. Обычно рассматривают главное сечение, проходящее через световой луч.

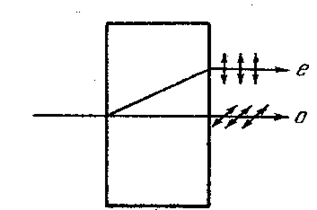
Исследование обыкновенного и необыкновенного лучей показывает, что оба луча полностью поляризованы во взаимно-перпендикулярных направлениях (рис. 5.4.6).

Плоскость колебаний обыкновенного луча перпендикулярна к главному сечению кристалла. В необыкновенном луче колебания светового вектора совершаются в плоскости, совпадающей с главным сечением. По выходе из кристалла оба луча отличаются друг от друга только направлением поляризации.

В некоторых кристаллах один из лучей поглощается сильнее другого. Это явление называется дихроизмом. Очень сильным дихроизмом в видимых лучах обладает кристалл турмалина. В нём обыкновенный луч практически полностью поглощается на длине 1 мм. В кристаллах сульфата йодистого хинина один из лучей поглощается на пути примерно в 0,1 мм.

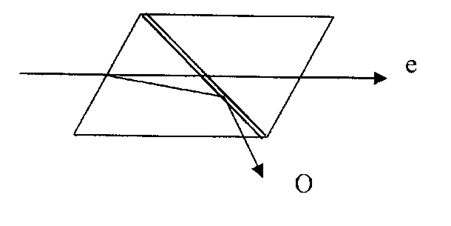
На явлении двойного лучепреломления основано действие поляризационного устройства, называемого призмой Николя (или просто николем). Оно представляет собой призму из исландского шпата (рис. 5.4.7), разрезанную по диагонали и склеенную канадским бальзамом.

Показатель преломления n канадского бальзама лежит между показателями преломления обыкновенного и необыкновенного лучей в исландском шпате (n0 > n > ne). Угол падения подбирается таким, чтобы обыкновенный луч претерпевал на прослойке бальзама полное внутреннее отражение и отклонялся в сторону, необыкновенный же луч свободно проходил через эту прослойку и выходил из призмы.

Отметим, что поляризационное устройство, используемое для исследования характера поляризации света, называется анализатором.

Двойное лучепреломление объясняется анизотропией кристаллов. В кристаллах некубической системы диэлектрическая проницаемость ε оказывается зависящей от направления. В одноосных кристаллах ε в направлении оптической оси и в направлениях, перпендикулярных к ней, имеет значения εII и ε⊥. В других направлениях ε имеет промежуточные значения. Если откладывать из некоторой точки отрезки, длина которых равна значению ε в данном направлении, то концы отрезков образуют эллипсоид вращения, ось которого совпадает с оптической осью кристалла. Согласно (5.2.4), . Следовательно, из анизотропии ε вытекает, что световым волнам с различными направлениями колебаний вектора соответствуют разные значения показателя преломления n. Поэтому скорость световых волн зависит от направления колебаний светового вектора .

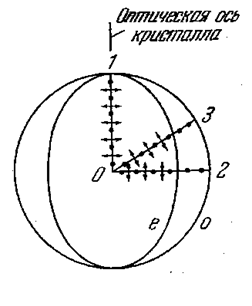
В обыкновенном луче колебания светового вектора происходят в направлении, перпендикулярном главному сечению кристалла (на рис. 5.4.8 эти колебания изображены точками на соответствующем луче). Поэтому при любом направлении обыкновенного луча (на рис. 5.4.8 указаны три направления 1,2,3) вектор образует с оптической осью кристалла прямой угол, и скорость световой волны будет одна и та же, равная . Изображая скорость обыкновенного луча в виде отрезков, отложенных по разным направлениям, получим сферическую поверхность. На рис. 5.4.8 показано пересечение этой поверхности с плоскостью чертежа. Представим, что в точке О внутри кристалла помещается точечный источник света. Тогда построенная нами сфера будет волновой поверхностью обыкновенных лучей.

Колебания в необыкновенном луче совершаются в главном сечении. Поэтому для разных лучей направления колебаний вектора (на рис. 5.4.8 эти направления изображены двусторонними стрелками) образуют с оптической осью разные углы α. Для луча 1 угол , вследствие чего скорость имеет значение , для луча 2 угол α = 0 и скорость равна . Для луча 3 скорость имеет промежуточное значение. Можно доказать, что волновая поверхность необыкновенных лучей представляет собой эллипсоид вращения.

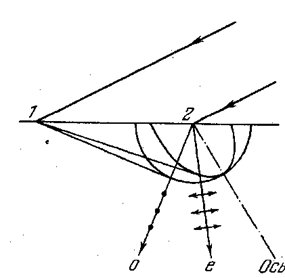
Ход обыкновенного и необыкновенного лучей в кристалле можно определить с помощью принципа Гюйгенса. На рис. 5.4.9 построены волновые поверхности обыкновенного и необыкновенного лучей с центром в точке 2, лежащей на поверхности кристалла. Построение выполнено для момента времени, когда волновой фронт падающей плоской волны достигает точки 1. Огибающие всех вторичных волн (волны, центры которых лежат в промежутке между точками 1 и 2, на рисунке не показаны) для обыкновенного и необыкновенного лучей, очевидно, представляют собой плоскости. Преломлённые лучи о и е, вышедшие из точки 2, проходят через точку касания огибающей с соответствующей волновой поверхностью. Из рис. 5.4.9 следует, что обыкновенный луч о совпадает с нормалью к соответствующей волновой поверхности. Необыкновенный же луч е заметно отклоняется от нормали к волновой поверхности.

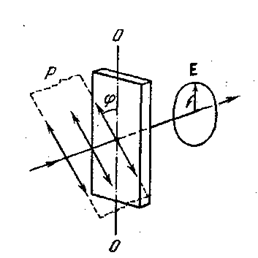
Рассмотрим кристаллическую пластинку, вырезанную параллельно оптической оси. При нормальном падении плоскополяризованного света на такую пластинку из неё выйдут два когерентных луча, поляризованных во взаимно-перпендикулярных направлениях. Отношение амплитуд этих лучей зависит от угла φ между плоскостью колебаний в падающем луче и оптической осью пластинки (рис. 5.4.10).

При φ = π/4 амплитуды будут одинаковыми. Поскольку обыкнов енный и необыкновенный лучи распространяются с разной скоростью, между ними возникает разность фаз, зависящая от толщины пластинки и разности показателей преломления n0 - ne. Пластинка, у которой возникающая при прохождении через неё разность хода лучей о и е равна λ/4 (соответственно разность фаз π/2). В этом случае конец результирующего вектора движется по эллипсу. Следовательно, вышедший из пластинки свет будет эллиптически поляризованным.

В частном случае, когда φ = 45°, свет будет поляризован по кругу.

На свойстве пластинки в четверть волны основан способ получения эллиптически поляризованного света (и света, поляризованного по кругу). Он заключается в последовательном пропускании естественного света через поляризатор и пластинку в четверть волны. Вращая пластинку вокруг направления луча, можно изменять отношение полуосей эллипса. Отметим, что при φ = 0 или π/2 из пластинки выходит плоскополяризованный свет.

к к к