ФИЗИКА
5.4.1. Естественный и поляризованный свет
В естественном свете колебания векторов ![]() и
и 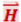 различных перпендикулярных к лучу направлений быстро и беспорядочно сменяют друг друга. Поэтому все направления колебаний равновероятны. Свет, у которого направления колебаний упорядочены каким-либо образом, называется поляризованным. Если колебания светового вектора происходят только в одной проходящей через луч плоскости, свет называется плоско-(или линейно-) поляризованным. Упорядоченность колебаний может заключаться в том, что вектор
различных перпендикулярных к лучу направлений быстро и беспорядочно сменяют друг друга. Поэтому все направления колебаний равновероятны. Свет, у которого направления колебаний упорядочены каким-либо образом, называется поляризованным. Если колебания светового вектора происходят только в одной проходящей через луч плоскости, свет называется плоско-(или линейно-) поляризованным. Упорядоченность колебаний может заключаться в том, что вектор ![]() поворачивается вокруг луча, одновременно пульсируя по величине. В результате конец вектора
поворачивается вокруг луча, одновременно пульсируя по величине. В результате конец вектора ![]() описывает эллипс. Такой свет называется эллиптически поляризованным. Если конец вектора
описывает эллипс. Такой свет называется эллиптически поляризованным. Если конец вектора ![]() описывает окружность, свет называется поляризованным по кругу.
описывает окружность, свет называется поляризованным по кругу.
Рассмотрим два взаимно перпендикулярных электрических колебания, совершающихся вдоль осей х и y и отличающихся по фазе на δ:
(5.4.1)
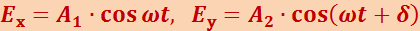 .
.
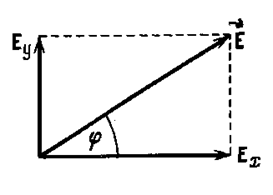
Результирующая напряжённость ![]() является векторной суммой напряжённостей Ex и Ey (рис. 5.4.1а). Угол φ между направлением вектора
является векторной суммой напряжённостей Ex и Ey (рис. 5.4.1а). Угол φ между направлением вектора ![]() и осью х определяется соотношением
и осью х определяется соотношением
(5.4.2)
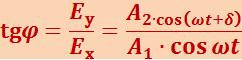 .
.
а) |
б) |
Рис. 5.4.1 |
|
Если разность фаз δ претерпевает случайные хаотические изменения, то и угол φ, т.е. направление светового вектора ![]() , будет испытывать скачкообразные неупорядоченные изменения. Следовательно, естественный свет можно представить как наложение двух некогерентных световых волн, поляризованных во взаимно-перпендикулярных плоскостях и имеющих одинаковую интенсивность. Такое представление упрощает рассмотрение прохождения света через поляризованные устройства.
, будет испытывать скачкообразные неупорядоченные изменения. Следовательно, естественный свет можно представить как наложение двух некогерентных световых волн, поляризованных во взаимно-перпендикулярных плоскостях и имеющих одинаковую интенсивность. Такое представление упрощает рассмотрение прохождения света через поляризованные устройства.
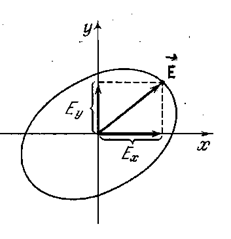
Теперь допустим, что накладывающиеся поляризованные во взаимно-перпендикулярных плоскостях световые волны когерентны. В этом случае при сложении взаимно-перпендикулярных электрических колебаний Ex и Ey, совершающихся с постоянной разностью фаз (т.е. когерентных), конец результирующего вектора Е в общем случае движется по эллипсу (см. рис. 5.4.1б), в частности, может получиться движение по прямой или окружности. Следовательно, две плоскополяризованные световые волны, плоскости колебаний которых взаимно-перпендикулярны, при наложении друг на друга дают эллиптически поляризованную световую волну. При разности фаз δ, равной нулю или π, эллипс вырождается в прямую и получается плоскополяризованный свет. При δ = ± π/2 и равенстве амплитуд складываемых волн эллипс превращается в окружность – получается свет, поляризованный по кругу. В зависимости от направления вращения вектора ![]() различают правую и левую эллиптическую и круговую поляризацию.
различают правую и левую эллиптическую и круговую поляризацию.
Плоскость, в которой колеблется световой вектор в плоскополяризованной волне, называется плоскостью колебаний, или плоскостью поляризации.
Плоскополяризованный свет можно получить из естественного с помощью приборов, называемых поляризаторами. Эти приборы свободно пропускают колебания, параллельные плоскости, которую называют плоскостью поляризатора, и полностью или частично задерживают колебания, перпендикулярные к этой плоскости. Поляризатор, задерживающий перпендикулярные к плоскости поляризатора колебания только частично, называется несовершенным. На выходе из такого поляризатора получается свет, в котором колебания одного направления преобладают над колебаниями других направлений. Такой свет называется частично поляризованным.
Если пропустить частично поляризованный свет через поляризатор, то при вращении прибора вокруг направления луча интенсивность прошедшего света будет изменяться в пределах от Imax до Imin, причём переход от одного из этих значений к другому будет совершаться при повороте на угол, равный π/2. Выражение
(5.4.3)
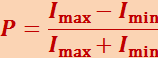
называется степенью поляризации. К эллиптически поляризованному свету понятие степени поляризации неприменимо (у такого света колебания полностью упорядочены).
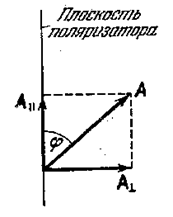
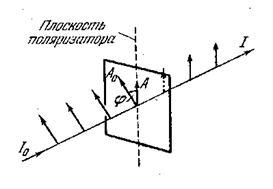
Плоскостью поляризатора угол φ, можно разложить на два колебания с амплитудами AII = A ⋅ cosφ и A⊥ = A ⋅ sinφ (рис. 5.4.2; луч перпендикулярен к плоскости рисунка). Первое колебание пройдёт через прибор, второе будет задержано. Интенсивность пропорциональна квадрату амплитуды. Поэтому если на поляризатор падает плоскополяризованный свет интенсивности I0, то интенсивность прошедшего света определяется соотношением
(5.4.4)

(рис. 5.4.3; φ – угол между плоскостью колебаний падающего света и плоскостью поляризатора).
Формула (5.4.4) носит название закона Малюса.
|
|
Рис. 5.4.2 |
Рис. 5.4.3 |
к к к