ФИЗИКА

2.1.1. Статистический способ описания коллектива

Состояние каждой частицы коллектива описывается заданием трёх её координат и трёх составляющих импульса. Составляя уравнения для частиц и решая их, можно, казалось бы, получить полные сведения о поведении системы и предсказать её состояние в любой момент времени. Однако подобные расчёты не только чрезвычайно сложны, но и бесполезны. Сложность задачи видна из того, что для описания поведения молекул газа, заключённых в 1 м3 при нормальных условиях, пришлось бы решать примерно 1026 связанных между собой уравнений движения с учётом начальных условий, что практически сделать невозможно. Однако если бы такое решение и было проведено, оно оказалось бы бесполезным, так как свойства системы, пришедшей в равновесие, не только не зависят от начальных значений координат и составляющих импульса, но и вообще остаются неизменными с течением времени, несмотря на то, что координаты и импульсы частиц непрерывно изменяются. Отсюда следует, что коллектив, как целое, является системой, качественно отличной от отдельных частиц и его поведение подчиняется иным закономерностям по сравнению с поведением отдельных частиц. Такими закономерностями являются статистические закономерности. В их существовании можно убедиться на следующих примерах.

Попадание данной молекулы газа в выделенный элемент объёма является делом случайным. Несмотря на это, в распределении молекул по объёму наблюдается чёткая закономерность: в равных элементах объёма содержится в среднем одинаковое число молекул.

Выпадание герба или решки при каждом бросании монеты является делом случайным. Тем не менее при большом числе бросаний выявляется вполне определённая закономерность: в среднем в половине бросаний выпадает герб и в половине – решка.

Такого рода закономерности и называются статистическими.

Основной особенностью статистических закономерностей является их вероятностный характер. Они позволяют предсказывать лишь вероятность наступления того или иного события или реализации того или иного результата. Так, в примере с бросанием монеты предсказываемая вероятность выпадания той или иной стороны равна 1/2. От этого значения вероятности могут быть и обязательно будут отступления в отдельных испытаниях, причём тем большие, чем меньше таких испытаний. В пяти подряд проведённых бросаниях монеты герб может появиться 3, 4 и даже 5 раз. Однако чем больше испытаний, т.е. чем больше членов коллектива, тем определённее и точнее становятся статистические предсказания. Расчёт показывает, что для системы, состоящей из N частиц, относительное отклонение наблюдаемой физической величины М (например, числа частиц в единице объёма) от её среднего значения 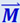обратно пропорционально √N:

(2.1.1)

.

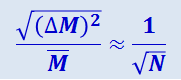С увеличением N отношение 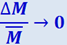и . При достаточно большом N величина . Так, в 1 м3 воздуха при нормальных условиях содержится в среднем 2,7⋅1025 молекул. Относительное отступление от этого числа в среднем равно

(2.1.2)

.

Это настолько ничтожное отклонение, что его невозможно обнаружить никакими приборами. Поэтому практически почти всегда приходится иметь дело с равномерным распределением молекул по объёму.

Следует, однако, подчеркнуть, что отступления от среднего значения не только могут быть, но и обязательно должны быть. Такие отступления называются флуктуациями.

Итак, в статистическом способе для описания поведения коллектива используются статистические закономерности. С их помощью наблюдаемые на опыте свойства тел (такие как давление и температура) истолковываются как суммарный, усреднённый результат действия отдельных молекул.

к к к