ФИЗИКА

5.2.2. Интерференция световых волн

Пусть две монохроматические волны одинаковой частоты, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания одинакового направления:

.

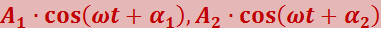Амплитуда результирующего колебания в данной точке определяется выражением

(5.2.8)

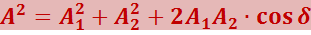
где δ = α2 - α1.

Если разность δ возбуждаемых волнами колебаний остаётся постоянной во времени, то волны называются когерентными.

В случае некогерентных волн δ непрерывно изменяется, принимая с равной вероятностью любые значения, вследствие чего среднее по времени значение cosδ равно нулю. Поэтому

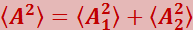
Отсюда, приняв во внимание соотношение (5.2.8), заключаем, что интенсивность, наблюдаемая при наложении некогерентных волн, равна сумме интенсивностей, создаваемых каждой из волн в отдельности:

(5.2.9)

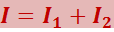
В случае когерентных волн cosδ имеет постоянное во времени (но своё для каждой точки пространства) значение, так что

(5.2.10)

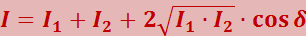
В тех точках пространства, для которых cosδ > 0, I  будет превышать I1 + I2; в точках, для которых cosδ < 0, I будет меньше I1 + I2. Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности. Это явление называется интерференцией волн. Особенно отчётливо проявляется интерференция в том случае, когда интенсивность обоих интерферирующих волн одинакова: I1 + I2. Тогда, согласно (2.10), в максимумах I = 4I1, в минимумах же I = 0. Для некогерентных волн при том же условии получается всюду одинаковая интенсивность: I = 2I1.

Из сказанного вытекает, что при освещении какой-либо поверхности несколькими источниками света должна, казалось бы, наблюдаться интерференционная картина с характерным для неё чередованием максимумов и минимумов интенсивности. Однако из повседневного опыта известно, что в указанном случае освещённость поверхности монотонно убывает по мере удаления от источников света и никакой интерференционной картины не наблюдается. Таким образом, волны, излучаемые независимыми источниками света, всегда некогерентны.

Когерентные световые волны можно получить, разделив (с помощью отражений или преломлений) волну, излучаемую одним источником на две части. Если заставить эти две волны пройти разные оптические пути, а потом наложить их друг на друга, то возникнет интерференция. Разность оптических длин путей, проходимых интерферирующими волнами, не должна быть очень большой, так как складывающиеся колебания должны принадлежать одному и тому же результирующему цугу волн. Если эта разность будет порядка 1 м, наложатся колебания, соответствующие разным цугам, и интерференции не будет.

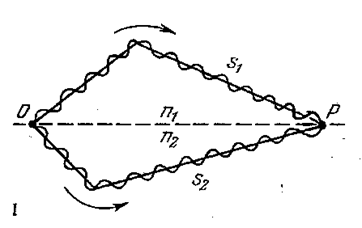
Пусть разделение на две когерентные волны происходит в точке О (рис. 5.2.1). До точки Р первая волна проходит в среде с показателем преломления n1 путь s1, вторая волна проходит в среде с показателем преломления n2 путь s2. Если в точке О фаза колебания равна ωt, то первая волна возбудит в точке Р колебание , а вторая волна – колебание , ( и – фазовые скорости волн).

Следовательно, разность фаз колебаний, возбуждаемых в точке Р, будет равна

Заменив ω/c через 2πν/c = 2π/λ0 (λ0 – длина волны в вакууме), выражению для разности фаз можно придать вид

(5.2.11)

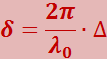
где

(5.2.12)

есть величина, равная разности оптических длин проходимых волнами путей (оптическая разность хода).

Из (5.2.11) следует, что если оптическая разность хода равна целому числу длин волн в вакууме

(5.2.13)

то разность фаз δ оказывается кратной 2π и колебания, возбуждаемые в точке Р обеими волнами, будет происходить с одинаковой фазой.

Таким образом, (5.2.13) есть условие интерференционного максимума.

Если Δ равна полуцелому числу длин волн в вакууме,

(5.2.14)

,

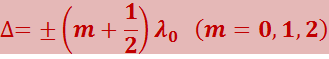то δ = ± (2m + 1)π, так что колебания в точке Р находятся в противофазе.

Значит, (5.2.14) есть условие интерференционного минимума.

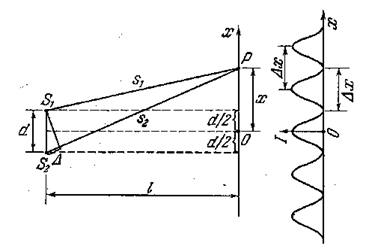
Рассмотрим две цилиндрические когерентные световые волны, исходящие из источников s1 и s2, имеющих вид параллельных тонких светящихся нитей либо узких щелей (рис. 5.2.2).

Область, в которой эти волны перекрываются, называется полем интерференции. Во всей этой области наблюдается чередование мест с максимальной и минимальной интенсивностью света. Если в поле интерференции внести экран, то на нём будет видна интерференционная картина, имеющая вид чередующихся светлых и тёмных полос. Вычислим ширину этих полос в предположении, что экран параллелен плоскости, проходящей через источники s1 и s2. Положение точки на экране будем характеризовать координатой х, отсчитываемой в направлении, перпендикулярном к линиям s1 и s2. Начало отсчёта выберем в точке О. Источники будем считать колеблющимися в одинаковой фазе. Из рис. 5.2.2 видно, что

.

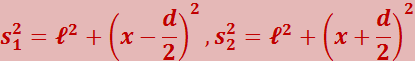Следовательно,

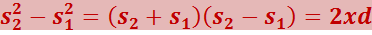
Для получения различимой интерференционной картины расстояние между источниками должно быть значительно меньшее. Расстояние х, в пределах которого образуются интерференционные полосы, также бывает значительно меньше ℓ. В этих условиях можно положить s2 + s1 = 2ℓ. Тогда 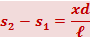. Умножив s2 - s1 на показатель преломления среды n, получим оптическую разность хода

(5.2.15)

.

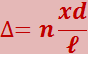Подстановка этого значения Δ в условие (5.2.13) даёт, что максимумы интенсивности будут наблюдаться при значениях х, равных

(5.2.16)

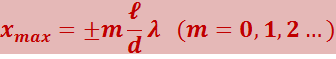
Здесь – длина волны в среде, заполняющей пространство между источниками и экраном.

Подставив (5.2.15) в условие (5.2.14), получим координаты минимумов интенсивности:

(5.2.17)

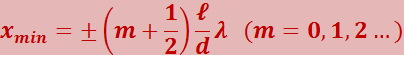
Назовём расстояние между двумя соседними максимумами интенсивности расстоянием между интерференционными полосами, а расстояние между соседними минимумами интенсивности – шириной интерференционной полосы.

Из формул (5.2.15) и (5.2.16) следует, что расстояние между полосами и ширина полосы имеют одинаковое значение, равное

(5.2.18)

Согласно (5.2.18), расстояние между полосами растёт с уменьшением расстояния между источниками d. При d, сравнимом с ℓ, расстояние между полосами было бы того же порядка, что и λ. В этом случае отдельные полосы были бы неразличимы. Для того чтобы интерференционная картина стала отчётливой, необходимо, чтобы выполнялось условие d<<ℓ.

Если интенсивность интерферирующих волн одинакова (I1 = I2 = I0), то согласно (2.10) результирующая интенсивность в точках, для которых разность фаз равна δ, определяется выражением

(5.2.19)

Поскольку δ, пропорциональна Δ, то, в соответствии с (5.2.15), δ растёт пропорционально х. Следовательно, интенсивность изменяется вдоль экрана по закону квадрата косинуса. Справа на рис. 5.2.2 показана зависимость I от х, получающаяся в монохроматическом свете.

Ширина интерференционных полос и расстояние между ними зависят от длины волны λ. Только в центре картины, при x = 0, совпадают максимумы всех длин волн. По мере удаления от центра картины максимумы разных цветов смещаются друг относительно друга всё больше и больше.

Измерив расстояние между полосами Δδ и зная ℓ и d, можно по формуле (5.2.18) вычислить λ. Именно из опытов по интерференции света были впервые определены длины волн для лучей разного цвета.

Когерентность. Различают временную и пространственную когерентность.

Временная когерентность. Описанный процесс интерференции двух когерентных световых волн является идеализированным. В действительности этот процесс гораздо сложнее. Это обусловлено тем, что монохроматическая волна, описываемая выражением A ⋅ cos(ωt - kr + α), в природе не существует. Всякая же реальная световая волна слагается из волн, испускаемых многими атомами.

Процесс излучения отдельного атома продолжается около 10-8 c. За это время успевает образоваться световая волна (цуг волн) протяжённостью примерно 3 м. «Погаснув», атом через некоторое время «вспыхивает» вновь. Но фаза нового цуга никак не связана с фазой предыдущего. В испускаемой телом световой волне излучение одной группы атомов через время порядка 10-8 c сменяется излучением другой группы, при этом фаза результирующей волны претерпевает случайные изменения.

Сменяет друг друга в данной точке пространства в данный момент времени относительно небольшое число цугов. Основная масса цугов проходит через рассматриваемую точку, не прерываясь. Поэтому фаза волны, образованной наложением огромного числа цугов, порождаемых отдельными атомами, не может совершать больших скачков. Она изменяется случайным образом небольшими шагами.

Когда некоторая величина х изменяется скачками, равными b, причём приращения +b и –b являются равновероятными, то говорят, что эта величина совершает случайные блуждания. Можно показать, что величина, совершающая случайные блуждания, в среднем всё больше удаляется от первоначального значения.

То же самое происходит и в том случае, если «шаги», совершаемые при случайных блужданиях, неодинаковы.

Фаза волны совершает случайные блуждания. Время tког., за которое случайное изменение фазы волны достигает значения порядка π, называется временем когерентности. За это время колебание как бы забывает свою первоначальную фазу и становится некогерентным по отношению к самому себе.

Соответствующий расчёт даёт, что время когерентности обратно интервалу частот Δν, представленных в данной световой волне:

(5.2.20)

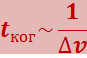
(знак «~» означает «по порядку величины равно»).

Из соотношения (5.2.20) следует, чем шире интервал частот, представленных в данной световой волне, тем меньше время когерентности этой волны. Для монохроматической волны Δν = 0 и время когерентности бесконечно велико.

Расстояние ℓког. = ctког., на которое перемещается волна за время когерентности, называется длиной когерентности (или длиной цуга). Длина когерентности − это то расстояние, на котором случайное изменение фазы достигает значения порядка π.

Частота связана с длиной волны в вакууме соотношением ν = с/λ0. Продифференцировав это соотношение, найдём, что Δν = с ⋅ Δλ0/λ02 (знак минус, получающийся при дифференцировании, мы опустим, кроме того, положим λ0 ≈ λ). Подставив Δν в (5.2.20), получим для времени когерентности выражение

(5.2.21)

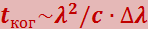
Отсюда

(5.2.22)

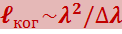
Пространственная когерентность. В реальной световой волне амплитуда и фаза колебаний изменяются не только вдоль направления распространения волны, но и в плоскости, перпендикулярной к этому направлению. Случайные изменения разности фаз в двух точках этой плоскости увеличиваются с расстоянием между ними. Расстояние ρког., на котором разность фаз достигает значения порядка π, называется длиной пространственной когерентности, или радиусом когерентности.

Нарушение пространственной когерентности обусловлено тем, что различные участки протяжённого источника света излучают несогласованно – со случайно изменяющейся разностью фаз. При прочих равных условиях длина пространственной когерентности уменьшается при увеличении размеров источника.

Если источник имеет форму диска, диаметр которого виден из данной точки под углом φ, то, как показывают расчёты,

(5.2.23)

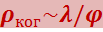
Для точечного источника φ = 0 и длина пространственной когерентности бесконечно велика.

Угловой размер Солнца составляет около 0,01 рад, длина световых волн примерно 5000 E. Следовательно, радиус когерентности приходящих от Солнца световых волн

.

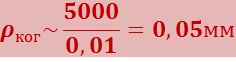Радиус когерентности световой волны вблизи поверхности излучающего её тела составляет несколько длин волн. По мере удаления от источника длина пространственной когерентности возрастает. Излучение лазера обладает огромной временной и пространственной когерентностью. У выходного отверстия лазера пространственная когерентность наблюдается во всём поперечном сечении светового пучка.

к к к