ФИЗИКА
В волновой оптике рассматриваются оптические явления, в которых проявляется волновая природа света (интерференция, дифракция, поляризация и дисперсия света). Так как свет представляет собой электромагнитные волны, то в основе волновой оптики лежат уравнения Максвелла и вытекающие из них соотношения для электромагнитных волн. В классической волновой оптике рассматриваются среды, линейные по своим оптическим свойствам, т.е. такие, диэлектрическая и магнитная проницаемость которых не зависит от интенсивности света. Поэтому в волновой оптике справедлив принцип суперпозиции волн.
Явления, наблюдающиеся при распространении света в оптически нелинейных средах, исследуются в нелинейной оптике. Нелинейные оптические эффекты становятся существенными при очень больших интенсивностях света, излучаемого мощными лазерами.
В электромагнитной волне колеблются векторы 
и 
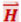. Как показывает опыт, физиологическое, фотохимическое и другие действия света вызываются колебаниями электрического вектора. В соответствии с этим в дальнейшем мы будем говорить о световом векторе, подразумевая под ним вектор напряжённости электрического поля. О магнитном векторе световой волны мы упоминать почти не будем.
Модуль амплитуды светового вектора будем обозначать, как правило, буквой А (иногда Em). Соответственно изменение во времени и пространстве проекции светового вектора на направление, вдоль которого он колеблется, будет описываться уравнением
(5.2.1)
Здесь k – волновое число;
r – расстояние, отсчитываемое вдоль направления распространения световой волны.
Для плоской волны в непоглощающей среде A = const, для сферической волны А убывает как 1/r.
Абсолютный показатель преломления среды определяется соотношением
(5.2.2)
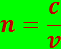
где ν – фазовая скорость волны в данной среде.
Из волнового уравнения для электромагнитных волн следует, что
(5.2.3)
.
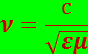Подставляя (5.2.3) в (5.2.2), получим
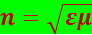
Для подавляющего большинства прозрачных веществ μ практически не отличается от единицы. Поэтому можно считать, что
(5.2.4)
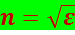
Формула (5.2.4) связывает оптические свойства вещества с его электромагнитными свойствами. Длины волн видимого света заключены в пределах
.
Указанные значения относятся к световым волнам в вакууме. В веществе длины световых волн будут иными. В случае колебаний частоты ν длина волны в вакууме равна λ0 = c/ν. В среде, в которой фазовая скорость световой волны ν = c/n, длина волны имеет значение
(5.2.5)
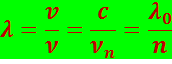
Частоты видимых световых волн лежат в пределах
.
Частота изменений вектора плотности потока энергии, переносимой волной, будет в 2 раза больше. Ни глаз, ни какой-либо иной приёмник световой энергии не может уследить за столь частыми изменениями потока энергии, вследствие чего они регистрируют усреднённый по времени поток. Модуль среднего по времени значения плотности потока энергии, переносимой световой волной, носит название интенсивности света I в данной точке пространства. Плотность потока электромагнитной энергии определяется вектором Пойнтинга 
. Следовательно,
(5.2.6)
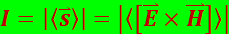
Усреднение производится за время «срабатывания» прибора, которое много больше периода колебаний волны. Измеряется интенсивность либо в ваттах, либо в люменах на 1 м2.
Можно показать, что интенсивность света пропорциональна показателю преломления среды и квадрату амплитуды световой волны.
Отсюда – при распространении света в однородной среде можно считать, что интенсивность пропорциональна квадрату амплитуды световой волны:
(5.2.7)
Несмотря на то, что световые волны поперечны, они обычно не обнаруживают асимметрии относительно луча. Это обусловлено тем, что в естественном свете (т.е. в свете, испускаемом обычными источниками) имеются колебания, совершающиеся в самых различных направлениях, перпендикулярных к лучу.
к к к