ФИЗИКА
5.1.2. Центрированная оптическая система
Оптические системы обычно состоят из двух и более преломляющих поверхностей. Представляет интерес случай, когда центры всех поверхностей, входящих в состав оптической системы, лежат на одной прямой. Оптическая система, обладающая этим свойством, называется центрированной.
Прямая линия, на которой расположены центры всех поверхностей системы, называется главной оптической осью.
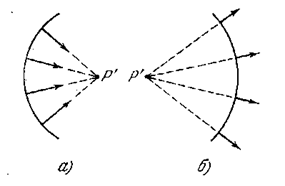
Всякая оптическая система осуществляет преобразование оптических пучков. Пучок образуется совокупностью лучей. Если лучи при своём продолжении пересекаются в одной точке, пучок называется гомоцентрическим. Гомоцентрическому пучку лучей соответствует сферическая волновая поверхность. На рис. 5.1.7а показан сходящийся, а на рис. 5.1.7б – расходящийся гомоцентрический пучок. Частным случаем гомоцентрического пучка является пучок параллельных лучей; ему соответствует плоская световая волна.
Рис. 5.1.7 |
Центрированная оптическая система обладает свойством сохранять гомоцентричность параксиального пучка независимо от числа преломляющих (или отражающих) поверхностей.
В этом случае лучи, вышедшие из точки Р, пересекутся в одной точке Р’. Эта точка представляет собой оптическое изображение точки Р. Если любая точка предмета изображается в виде точки, изображение называется точечным, или стигматическим.
Изображение называется действительным, если световые лучи в точке Р’ действительно пересекаются (см. рис. 5.1.7а) и мнимым, если в Р’ пересекаются продолжения лучей, проведённые в направлении, обратном направлению распространения света (см. рис. 5.1.7б).
Вследствие обратимости световых лучей источник света Р и изображение Р’ могут поменяться ролями – точечный источник, помещённый в Р’, будет иметь своё изображение в Р. По этой причине Р и Р’ называются сопряжёнными точками.
Оптическая система, которая даёт стигматическое изображение, геометрически подобное отображаемому предмету, называется идеальной. С помощью такой системы пространственная непрерывность точек Р отображается в виде пространственной непрерывности точек Р’. Первая непрерывность точек называется пространством предметов, вторая – пространством изображений. В обоих пространствах точки, прямые и плоскости однозначно соответствуют друг другу. Такое соотношение двух пространств называется в геометрии коллинеарным соответствием.
Среди бесконечного множества сопряжённых точек и сопряжённых плоскостей имеются точки и плоскости, обладающими особыми свойствами. Такие точки и плоскости называются кардинальными. К их числу относятся фокальные, главные и угловые точки и плоскости. Задание кардинальных точек или плоскостей полностью определяет свойства идеальной центрированной оптической системы.
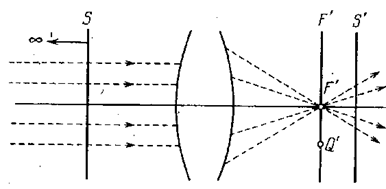
Фокальные плоскости и фокусы оптической системы. На рис. 5.1.8 показаны внешние преломляющие поверхности и оптическая ось некоторой идеальной центрированной оптической системы. Возьмём в пространстве предметов этой системы плоскость s, перпендикулярную к оптической оси. Из соображений симметрии следует, что сопряжённая с s плоскость s’ также перпендикулярна к оптической оси. Перемещение плоскости s относительно системы вызовет соответствующее перемещение плоскости s’. Когда плоскость s окажется очень далеко, дальнейшее увеличение её расстояния от системы практически не вызывает изменения положения плоскости s’. Это означает, что в результате удаления плоскости s на бесконечность плоскость s’ оказывается в определённом предельном положении F’. Плоскость F’, совпадающая с предельным положением плоскости s’, называется задней фокальной плоскостью оптической системы.
Рис. 5.1.8 |
Точка пересечения задней фокальной плоскости с оптической осью называется задним фокусом системы F’. Эта точка сопряжена с удалённой на бесконечность точкой Р∞, лежащей на оси системы. Лучи, выходящие из Р∞ , образуют параллельный оси пучок. По выходе из системы они образуют пучок, сходящийся в фокусе F’.
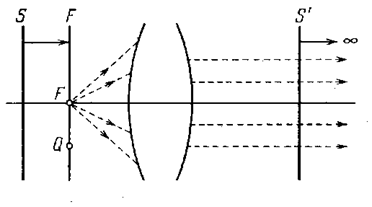
Если удалить на бесконечность перпендикулярную к оси плоскость s’ (рис. 5.1.9), сопряжённая с ней плоскость s придёт в предельное положение F, которое называется передней фокальной плоскостью системы.
Точка пересечения передней фокальной плоскости F с оптической осью называется передним фокусом системы F. Лучи, вышедшие из фокуса F, образуют после выхода из системы пучок параллельных оси лучей.
Рис. 5.1.9 |
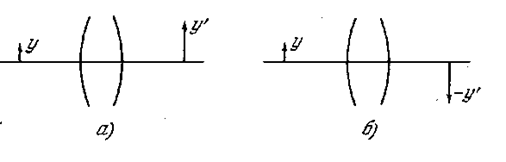
Главные плоскости и точки. Рассмотрим две сопряжённые плоскости, перпендикулярные к оптической оси системы. Отрезок прямой y (рис. 5.1.10), лежащий в одной из этих плоскостей, будет иметь своим изображением отрезок прямой y’, лежащий в другой плоскости (оба отрезка лежат в плоскости рисунка). Изображение y’ может быть обращено либо в ту же сторону, что и предмет y (см. рис. 5.1.10а), либо в противоположную сторону (см. рис. 5.1.10б).
Рис. 5.1.10 |
В первом случае изображение называется прямым, во втором – обратным. Отрезки, откладываемые от оптической оси вверх, принято считать положительными, откладываемые вниз – отрицательными.
Отношение линейных размеров изображения и предмета называется линейным, или поперечным, увеличением β:
(5.1.9)
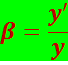
Линейное увеличение – алгебраическая величина.
Можно доказать, что существуют две такие сопряжённые плоскости, которые отображают друг друга с увеличением β = +1. Эти плоскости называются главными. Плоскость, принадлежащая пространству предметов, именуется передней главной плоскостью системы. Её обозначают буквой Н. Плоскость, принадлежащую пространству изображений, именуют задней главной плоскостью. Её обозначают Н’. Точки пересечения главных плоскостей с оптической осью называются главными точками системы. Их обозначают теми же символами Н и Н’. В зависимости от устройства системы главные плоскости и точки могут находиться как вне, так и внутри системы.
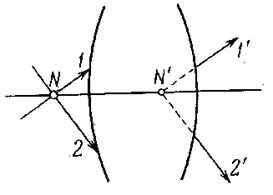
Узловые плоскости и точки. Узловыми точками или узлами называются лежащие на оптической оси сопряжённые точки N и N’, обладающие тем свойством, что проходящие через них сопряжённые лучи параллельны между собой (см. лучи 1 – 1'’;2 – 2’ на рис. 5.1.11). Перпендикулярные к оси плоскости, проходящие через узлы, называются узловыми плоскостями.
Рис. 5.1.11 |
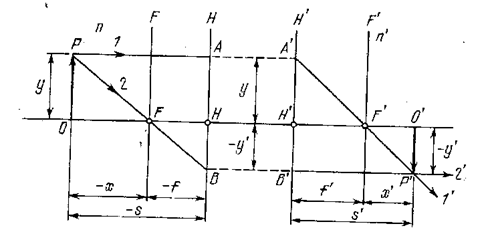
Формула системы. Задание кардинальных плоскостей или точек полностью определяет свойства оптической системы. В частности, зная положение кардинальных плоскостей, можно построить оптическое изображение, даваемое системой. Возьмём в пространстве предметов отрезок ОР, перпендикулярный к оптической оси (рис. 5.1.12). Положение этого отрезка можно задать либо расстоянием х, отсчитанным от точки F до точки О, либо расстоянием s от Н до О. Величины х и s, как и фокусные расстояния f и f ', являются алгебраическими (на рис. указываются их модули).
Рис. 5.1.12 |
Проведём из точки Р луч 1, параллельный оптической оси. Он пересечёт плоскость Н в точке А. В соответствии со свойствами главных плоскостей сопряжённый лучу 1 луч 1' должен проходить через сопряжённую с точкой А точку А' плоскости H'. Так как луч 1 параллелен оптической оси, сопряжённый с ним луч 1' пойдёт через задний фокус F'. Теперь проведём из точки Р луч 2, проходящий через передний фокус F. Он пересечёт плоскость Н в точке В. Сопряжённый с ним луч 2' пройдёт через сопряжённую с В точку В' плоскости Н' и будет параллельным оптической оси. Точка Р' пересечения лучей 1' и 2' представляет собой изображение точки Р. Изображение О'Р', как и отрезок ОР, перпендикулярно к оптической оси.
Положение изображения О'Р' можно охарактеризовать либо расстоянием х' от точки F' до точки О', либо расстоянием s' от Н' до О'. Величины х' и s' являются алгебраическими. В случае, изображённом на рис. 5.1.12, они положительны.
Величина х', определяющая положение изображения, связана с величиной х, определяющей положение предмета, и с фокусными расстояниями f и f ' формулой Ньютона
(5.1.10)

Если n = n', то формула Ньютона приобретает вид
(5.1.11)

Обе формулы Ньютона представляют собой формулы центрированной оптической системы.
Линза. Самой простой центрированной оптической системой является линза. Она состоит из двух поверхностей, ограничивающих прозрачный (обычно стекло) материал, одна из которых обязательно является сферической, а другая может быть сферической или плоской. В зависимости от вида ограничивающих поверхностей линзы бывают двояковыпуклыми, плосковыпуклыми, выпукло-вогнутыми, двояковогнутыми, плосковогнутыми и вогнуто-выпуклыми (рис. 5.1.13). Легко убедиться, что линзы I, II, III являются собирательными, а линзы IV, V, VI – рассеивающими, если их материал оптически плотнее, чем окружающая среда. В противоположном случае линзы I, II, III являются рассеивающими, а линзы IV, V, VI – собирательными.
Рис. 5.1.13 |
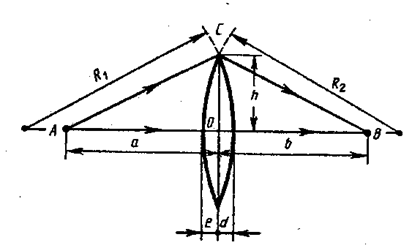
Рассмотрим двояковыпуклую линзу (рис. 5.1.14). Линза называется тонкой, если её толщина (расстояние между ограничивающими поверхностями) значительно меньше по сравнению с радиусами поверхностей, ограничивающих линзу. Прямая, проходящая через центры кривизны поверхностей линзы, называется главной оптической осью. Для всякой линзы существует точка, называемая оптическим центром линзы, лежащая на главной оптической оси и обладающая тем свойством, что лучи проходят сквозь неё, не преломляясь. Для простоты будем считать, что оптический центр совпадает с геометрическим центром средней части линзы.
Рис. 5.1.14 |
На основе принципа Ферма нетрудно получить формулу тонкой линзы
(5.1.12)
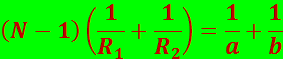
Здесь ![]() – относительный показатель преломления (n и n1 – соответственно абсолютные показатели преломления линзы и окружающей среды). Радиус кривизны выпуклой поверхности линзы считается положительным, вогнутой – отрицательным.
– относительный показатель преломления (n и n1 – соответственно абсолютные показатели преломления линзы и окружающей среды). Радиус кривизны выпуклой поверхности линзы считается положительным, вогнутой – отрицательным.
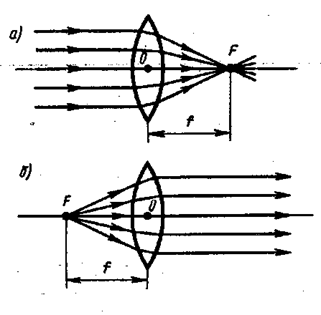
Если a = ∞, т.е. лучи падают на линзу параллельным пучком (рис. 5.1.15), то
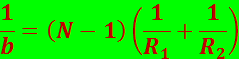
Соответствующее этому случаю расстояние b = OF = f называется фокусным расстоянием линзы, определяемым по формуле
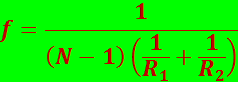 .
.
Рис. 5.1.15 |
Если b = ∞, т.е. изображение находится в бесконечности и, следовательно, лучи выходят из линзы параллельным пучком (см. рис. 5.1.15), то a = OF = f. Таким образом, фокусные расстояния линзы, окружённой с обеих сторон одинаковой средой, равны. Точки F, лежащие по обе стороны линзы на расстоянии, равном фокусному, называются фокусами линзы. Фокус – это точка, в которой после преломления собираются все лучи, падающие на линзу параллельно главной оптической оси. Величина
(5.1.13)
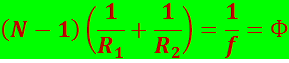
называется оптической силой линзы. Её единица – диоптрия (ДПТР). Диоптрия – оптическая сила линзы с фокусным расстоянием 1 м; 1 ДПТР = 1/м.
Линзы с положительной оптической силой являются собирающими, с отрицательной – рассеивающими. Плоскости, проходящие через фокусы линзы перпендикулярно её главной оптической оси, называются фокальными плоскостями. В отличие от собирающей рассеивающая линза имеет мнимые фокусы. В мнимом фокусе сходятся (после преломления) воображаемые продолжения лучей, падающих на рассеивающую линзу параллельно главной оптической оси. Учитывая (5.1.13), формулу линзы можно записать в виде
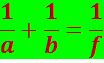 .
.
Для рассеивающей линзы расстояния f и b надо считать отрицательными.
Построение изображения предмета в линзах осуществляется с помощью следующих лучей:
- луча, проходящего через оптический центр линзы и не изменяющего своего направления;
- луча, идущего параллельно главной оптической оси; после преломления в линзе этот луч (или его продолжение) проходит через второй фокус линзы;
- луча (или его продолжения), проходящего через первый фокус линзы; после преломления в ней он выходит из линзы параллельно её главной оптической оси.
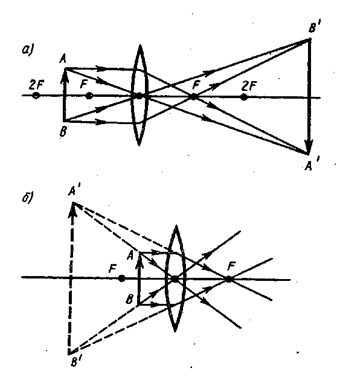
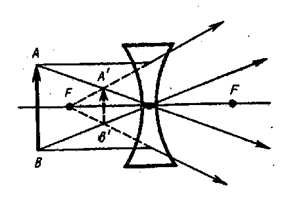
Для примера приведём построения изображений в собирающей (рис. 5.1.16) и в рассеивающей (рис. 5.1.17) линзах: действительное (см. рис. 5.1.16а) и мнимое (см. рис. 5.1.16б) изображения – в собирающей линзе, мнимое – в рассеивающей.
|
|
Рис. 5.1.16 |
Рис. 5.1.17 |
Отношение линейных размеров изображения и предмета называется линейным увеличением линзы. Отрицательным значениям линейного увеличения соответствует действительное изображение (оно перевёрнутое), положительным – мнимое изображение (оно прямое).
В заключение надо сказать, что линза является далеко не идеальной оптической системой. Даваемые ею изображения предметов обладают рядом погрешностей.
к к к