ФИЗИКА
5.1.1. Законы геометрической оптики
Основу геометрической оптики образуют четыре закона:
1) закон прямолинейного распространения света;
2) закон отражения света;
3) закон преломления света;
4) закон независимости световых лучей.
Закон прямолинейного распространения утверждает, что в однородной среде свет распространяется прямолинейно. Этот закон является приближённым: при прохождении света через очень малые отверстия наблюдаются отклонения от прямолинейности, тем бóльшие, чем меньше отверстие.
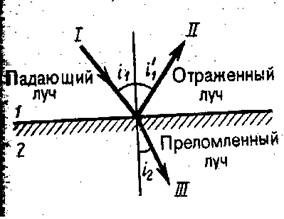
Законы отражения и преломления определяют направления отражённого II и преломлённого III лучей при падении луча I света на границу раздела двух прозрачных сред (рис. 5.1.1).
Рис. 5.1.1 |
Закон отражения: отражённый луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведённым к границе раздела двух сред в точке падения; угол 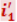 отражения равен углу
отражения равен углу 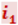 падения.
падения.
Закон преломления: луч падающий, луч преломлённый и перпендикуляр, проведённый к границе раздела в точке падения, лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления равно отношению абсолютных показателей преломления второй среды к первой:
(5.1.1)
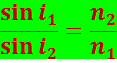
Абсолютный показатель преломления показывает, во сколько раз скорость распространения света в данной среде меньше, чем скорость света в вакууме:
(5.1.2)
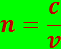
Для любой среды ![]() . Из (5.1.2) следует, чем больше абсолютный показатель преломления среды, тем меньше скорость распространения света в ней. При сравнении абсолютных показателей преломления двух сред используют понятие оптической плотности среды.
. Из (5.1.2) следует, чем больше абсолютный показатель преломления среды, тем меньше скорость распространения света в ней. При сравнении абсолютных показателей преломления двух сред используют понятие оптической плотности среды.
Оптически более плотная среда – среда с бóльшим показателем преломления.
Оптически менее плотная среда – среда с меньшим показателем преломления.
Закон независимости световых лучей утверждает, что лучи при пересечении не возмущают друг друга, т.е. пересечения лучей не мешают каждому из них распространяться независимо друг от друга. Этот закон справедлив лишь при не слишком больших интенсивностях света. При интенсивностях, достигаемых с помощью лазеров, независимость световых лучей перестаёт соблюдаться.
Первые три закона вытекают из принципа Ферма. В формулировке самого Ферма принцип гласит, что свет распространяется по такому пути, для прохождения которого ему требуется минимальное время.
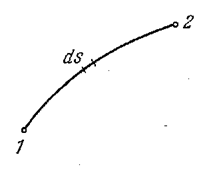
Для прохождения участка пути ds (рис. 5.1.2) свету требуется время ![]() , где v – скорость света в данной точке среды. Заменив v через c/n (5.1.2), получим, что dt=(1/c)ndc. Следовательно, время τ, затрачиваемое светом на прохождение пути от точки 1 до точки 2, равно
, где v – скорость света в данной точке среды. Заменив v через c/n (5.1.2), получим, что dt=(1/c)ndc. Следовательно, время τ, затрачиваемое светом на прохождение пути от точки 1 до точки 2, равно
(5.1.3)
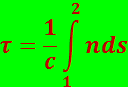
Рис. 5.1.2 |
Имеющая размерность длины величина
(5.1.4)
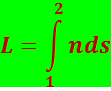
называется оптической длиной пути.
В однородной среде оптическая длина пути равна произведению геометрической длины пути s на показатель преломления среды n
(5.1.5)
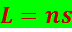
Согласно (5.1.3) и (5.1.4),
(5.1.6)
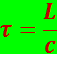
Пропорциональность времени прохождения τ оптической длине пути L даёт возможность сформулировать принцип Ферма следующим образом: свет распространяется по такому пути, оптическая длина которого минимальна. Точнее, оптическая длина пути должна быть экстремальной, т.е. либо минимальной, либо максимальной, либо стационарной – одинаковой для всех возможных путей.
В последнем случае все пути света между двумя точками оказываются таутохронными (требующими для своего прохождения одинакового времени).
Из принципа Ферма вытекает обратимость световых лучей. Действительно, оптический путь, который минимален в случае распространения света из точки 1 в точку 2, окажется минимальным и в случае распространения света в обратном направлении.
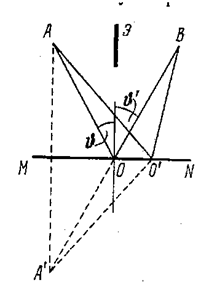
Получим с помощью принципа Ферма законы отражения и преломления света. Пусть свет попадает из точки А в точку В, отразившись от поверхности MN (рис. 5.1.3; прямой путь из А в В преграждён непрозрачным экраном Э). Среда, в которой проходит луч, однородна. Поэтому минимальность оптической длины пути сводится к минимальности его геометрической длины. Геометрическая длина произвольно взятого пути равна AO'B = AOB (вспомогательная точка A' является зеркальным изображением точки А). Из рисунка видно, что наименьшей длиной обладает путь луча, отразившегося в точке О, для которой угол отражения равен углу падения. Заметим, что при удалении точки O' от точки O геометрическая длина пути неограниченно возрастает, так что в данном случае имеется только один экстремум − минимум.
Рис. 5.1.3 |
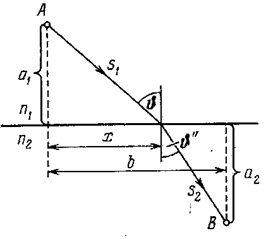
Теперь найдём точку, в которой должен преломиться луч, распространяясь от А к В, чтобы оптическая длина была экстремальной (рис. 5.1.4). Для произвольного луча оптическая длина пути L равна
 .
.
Рис. 5.1.4 |
Чтобы найти экстремальное значение, продифференцируем L по х и приравняем производную нулю:

Множители при n1 и n2 равны соответственно ![]() и
и ![]() . Таким образом, получается соотношение
. Таким образом, получается соотношение
(5.1.7)

выражающее закон преломления.
Если свет распространяется из среды с бóльшим показателем преломления n1 (оптически более плотной) в среду с меньшим показателем преломления n2 (оптически менее плотную), например, из стекла в воду, то, согласно (5.1.7),
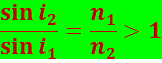 .
.
Отсюда следует, что преломлённый луч удаляется от нормали и угол преломления 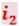 больше, чем угол падения (рис. 5.1.5а). С увеличением угла падения увеличивается угол преломления (см. рис. 5.1.5б) до тех пор, пока при некотором угле падения
больше, чем угол падения (рис. 5.1.5а). С увеличением угла падения увеличивается угол преломления (см. рис. 5.1.5б) до тех пор, пока при некотором угле падения ![]() угол преломления не окажется равным
угол преломления не окажется равным ![]() . Угол
. Угол ![]() называется предельным углом. При углах падения
называется предельным углом. При углах падения ![]() весь падающий свет полностью отражается (см. рис. 5.1.5в).
весь падающий свет полностью отражается (см. рис. 5.1.5в).
Рис. 5.1.5 |
По мере приближения угла падения к предельному интенсивность преломлённого луча уменьшается, а отражённого – растёт. Если ![]() , то интенсивность преломлённого луча обращается в нуль, а интенсивность отражённого равна интенсивности падающего. Таким образом, при углах падения в пределах от
, то интенсивность преломлённого луча обращается в нуль, а интенсивность отражённого равна интенсивности падающего. Таким образом, при углах падения в пределах от ![]() до
до ![]() луч не преломляется, а полностью отражается в первую средý, причём интенсивности отражённого и падающего лучей одинаковы. Это явление называется полным внутренним отражением.
луч не преломляется, а полностью отражается в первую средý, причём интенсивности отражённого и падающего лучей одинаковы. Это явление называется полным внутренним отражением.
Предельный угол ![]() определим из формулы (5.1.7) при подстановке в неё
определим из формулы (5.1.7) при подстановке в неё ![]() . Тогда
. Тогда
(5.1.8)
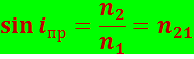
Уравнение (5.1.8) удовлетворяет значениям угла ![]() при
при ![]() . Следовательно, явление полного внутреннего отражения имеет место только при падении света из среды оптически более плотной в средý оптически менее плотную.
. Следовательно, явление полного внутреннего отражения имеет место только при падении света из среды оптически более плотной в средý оптически менее плотную.
Явление полного внутреннего отражения используется в призмах полного отражения. Показатель преломления стекла равен ![]() , поэтому предельный угол для границы «стекло – воздух» равен
, поэтому предельный угол для границы «стекло – воздух» равен ![]() . Поэтому при падении света на границу «стекло – воздух» при
. Поэтому при падении света на границу «стекло – воздух» при ![]() всегда будет иметь место полное внутреннее отражение. На рис. 1.6, а–в показаны призмы полного отражения, позволяющие:
всегда будет иметь место полное внутреннее отражение. На рис. 1.6, а–в показаны призмы полного отражения, позволяющие:
а) повернуть луч на 90°;
б) повернуть изображение;
в) обернуть лучи. Такие призмы применяются в оптических приборах (например, в биноклях, перископах), а также в рефрактометрах, позволяющих определять показатели преломления тел (по закону преломления, измеряя ![]() , находим относительный показатель преломления двух сред, а также абсолютный показатель преломления одной из сред, если показатель преломления другой среды известен).
, находим относительный показатель преломления двух сред, а также абсолютный показатель преломления одной из сред, если показатель преломления другой среды известен).
Рис. 5.1.6 |
Явление полного внутреннего отражения используется также в световодах, представляющих собой тонкие, произвольным образом изогнутые нити (волокна) из оптически прозрачного материала. В волоконных деталях применяют стеклянное волокно, световедущая жила (сердцевина) которого окружается стеклом – оболочкой из другого стекла с меньшим показателем преломления. Свет, падающий на торец световода под углами, бóльшими предельного, претерпевает на поверхности раздела сердцевины и оболочки полное отражение и распространяется только по световедущей жиле.
Таким образом, с помощью световодов можно как угодно искривлять путь светового пучка. Диаметр световедущих жил лежит в пределах от нескольких микрометров до нескольких миллиметров. Для передачи изображений, как правило, применяются многожильные световоды. Вопросы передачи световых волн и изображений изучаются в специальном отделе оптики – волоконной оптике. Световоды используются в электронно-лучевых трубках, в электронно-счётных машинах, для кодирования информации, в медицине (например, диагностика желудка), для целей интегральной оптики и т.д.
к к к