ФИЗИКА

4.3.6. Эффект Доплера для электромагнитных волн

Доплеровское смещение частоты световых волн определяется относительной скоростью источника и приёмника волн. Свяжем с приёмником света начало координат инерциальной системы отсчёта К, а с источником – начало координат системы K' (рис. 4.3.7).

Оси х и x' направим вдоль вектора скорости , с которой система K' (т.е. источник движется относительно системы К (т.е. приёмника). Уравнение плоской световой волны, испускаемой источником по направлению к приёмнику, в системе K' имеет вид

(4.3.31)

,

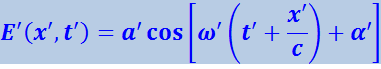где ω' - частота волны, наблюдаемая в системе отсчёта, связанной с источником, т.е. частота, с которой колеблется источник.

Полагаем, что световая волна распространяется в вакууме, поэтому фазовая скорость равна с. От источника к приёмнику волна распространяется в направлении, противоположном оси x', поэтому перед x'/c стоит знак плюс. В системе К эта же волна описывается уравнением

(4.3.32)

,

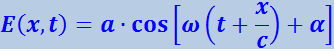где ω - частота, регистрируемая в системе К, т.е. частота, воспринимаемая приёмником.

Уравнение волны в системе К можно получить и из уравнения в системе K', перейдя от x' и t' к x и t с помощью преобразований Лоренца

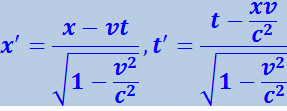
Подставив эти значения в (4.3.31), получим:

(4.3.33)

.

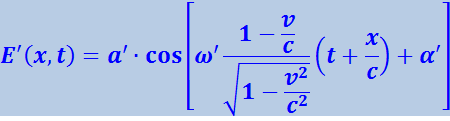Уравнения (4.3.32) и (4.3.33) описывают в системе К одну и ту же волну. Следовательно, должно выполняться соотношение

.

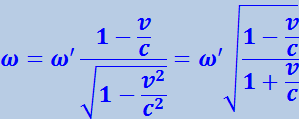Изменим обозначения: частоту источника ω' обозначим ω0, а скорость источника относительно приёмника обозначим буквой v. Тогда формула примет вид

(4.3.34)

.

Здесь скорость ν – величина алгебраическая. При удалении источника ν > 0 и согласно (4.3.34) ω < ω0; при приближении источника к приёмнику ν < 0 тогда ω > ω0.

Можно показать, что относительное изменение частоты

(4.3.35)

(Δω = ω - ω0).

Кроме продольного эффекта, для электромагнитных волн существует поперечный эффект Доплера. Он заключается в уменьшении регистрируемой приёмником частоты, наблюдающемся в том случае, когда вектор относительной скорости направлен перпендикулярно к прямой, проходящей через приёмник и источник (например, когда источник движется по окружности, в центре которой находится приёмник). В этом случае частота ω0 источника связана с частотой ω, регистрируемой приёмником, соотношением

(4.3.36)

.

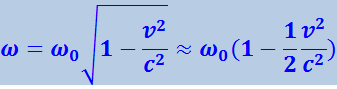Относительное изменение частоты при поперечном эффекте Доплера

(4.3.37)

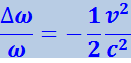
пропорционально квадрату отношения ν/c и, следовательно, значительно меньше, чем при продольном эффекте.

В общем случае относительную скорость можно разложить на две составляющие, одна из которых направлена вдоль луча, а другая – перпендикулярно лучу. Первая составляющая обусловит продольный, вторая поперечный эффект Доплера.

Продольный эффект Доплера используется для определения радиальной скорости звёзд. В частности, таким способом было обнаружено разбегание галактик.

к к к