ФИЗИКА

4.3.5. Излучение диполя

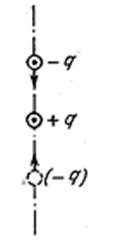
Простейшей системой, излучающей электромагнитные волны, является колеблющийся электрический диполь. Диполь – это система, образованная неподвижным точечным зарядом +q и колеблющимся около него точечным зарядом -q (рис. 4.3.4). Дипольный электрический момент этой системы изменяется со временем по закону

(4.3.25)

,

где - радиус-вектор заряда -q;

ℓ - амплитуда колебаний;

- единичный вектор, направленный вдоль оси диполя,

.

Изучение подобной излучающей системы особенно важно в связи с тем, что многие вопросы взаимодействия излучения с веществом могут быть объяснены классически, исходя из представления об атомах как о системах зарядов, в которых содержатся электроны, способные совершать гармонические колебания около положения равновесия.

Рассмотрим излучение диполя, размеры которого малы по сравнению с длиной волны (ℓ<<λ). Такой диполь называется элементарным. В непосредственной близости от диполя картина электромагнитного поля очень сложна. Она сильно упрощается в так называемой волновой зоне диполя, которая начинается на расстояниях r, значительно превышающих длину волны (r>>λ).

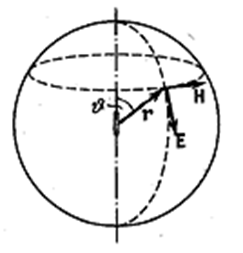
Если волна распространяется в однородной изотропной среде, то волновой фронт в волновой зоне будет сферическим. Векторы и 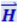в каждой точке взаимно перпендикулярны и перпендикулярны к лучу, т.е. радиусу-вектору, проведённому в данную точку из центра диполя. Если смотреть вдоль луча , то мгновенная картина волны будет такой же как на рис. 4.3.5, с тем отличием, что амплитуда вдоль луча будет постепенно убывать.

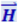В каждой точке и колеблются по закону cos(ωt - kr). Амплитуды и зависят от расстояния r до излучателя и от угла ϑ между направлением радиуса-вектора и осью диполя (рис. 4.3.5). Эта зависимость для вакуума имеет вид

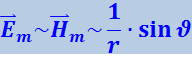
Среднее значение плотности потока энергии пропорционально произведению Em ⋅ Hm, следовательно,

(4.3.26)

.

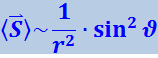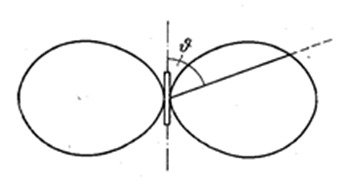
Из этой формулы следует, что интенсивность волны изменяется вдоль луча (при ϑ = const) обратно пропорционально квадрату расстояния от излучателя. Кроме того, она зависит от угла ϑ. Сильнее всего излучает диполь в направлениях, перпендикулярных к его оси (ϑ = π/2). В направлениях, совпадающих с осью (ϑ = 0 и π), диполь не излучает. Зависимость интенсивности от угла ϑ очень наглядно изображается с помощью диаграммы направленности диполя (рис. 4.3.6).

Эта диаграмма строится так, чтобы длина отрезка, отсекаемого её на луче, проведённом из центра диполя, давала интенсивность излучения под углом ϑ.

Расчёт даёт, что мощность излучения диполя Р пропорциональна квадрату второй производной дипольного момента по времени:

(4.3.27)

.

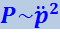Согласно формуле (4.3.25) . Подстановка этого выражения в (4.3.27) даёт

(4.3.28)

.

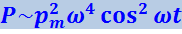Усреднив это выражение по времени, получим:

(4.3.29)

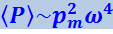
Таким образом, средняя мощность излучения диполя пропорциональна квадрату амплитуды электрического момента диполя и четвёртой степени частоты. Поэтому при малой частоте излучение электрических систем бывает незначительным.

Согласно формуле (4.3.25) , где ускорение колеблющегося заряда. Подстановка этого выражения в (4.3.27) даёт, что

(4.3.30)

.

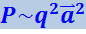Эта формула определяет мощность излучения не только при колебаниях, но и при произвольном движении заряда. Всякий заряд, движущийся с ускорением, возбуждает электромагнитные волны, причём мощность излучения пропорциональна квадрату заряда и квадрату ускорения.

Заряд, совершающий гармонические колебания излучает монохроматическую волну с частотой, равной частоте колебаний заряда. Если же ускорение заряда изменяется не по гармоническому закону, излучение состоит из набора волн различных частот.

Согласно формуле (4.3.30) интенсивность обращается в нуль при . Следовательно, электрон, движущийся равномерно, не излучает электромагнитных волн. Это, однако, справедливо лишь в том случае, если скорость электрона νэл. не превышает скорости света в той среде, в которой движется электрон. В случае, когда νэл. > νсв., наблюдается излучение, открытое П.А. Черенковым.

к к к