ФИЗИКА

4.3.4. Энергия электромагнитных волн и импульс электромагнитного поля

Электромагнитные волны переносят энергию. Плотность потока энергии можно получить, умножив плотность энергии на скорость волны.

Пусть электромагнитная волна распространяется в вакууме. В этом случае скорость волны равна с. Плотность энергии электромагнитного поля ω слагается из плотности энергии электрического поля и плотности энергии магнитного поля

(4.3.15)

(для вакуума ε = μ = 1).

В данной точке пространства векторы и 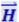изменяются в одинаковой фазе (это справедливо только для вакуума и непроводящей среды). Поэтому соотношение (4.3.13) между амплитудными значениями Е и Н справедливо и для их мгновенных значений

(4.3.16)

.

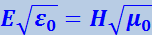Отсюда следует, что плотности энергии электрического и магнитного полей волны в каждый момент времени одинаковы: ωE = ωH.

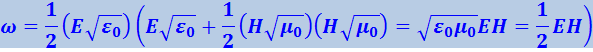
Умножив найденное уравнение на скорость волны с, получим модуль плотности потока энергии

.

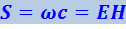Векторы и 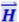взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему. Поэтому направление вектора совпадают с направлением переноса энергии, а модуль этого вектора равен E ⋅ H. Значит, вектор плотности потока электромагнитной энергии можно представить как векторное произведение и :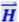

(4.3.17)

.

Вектор 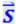называется вектором Пойтинга.

Можно показать, что формула (4.3.17) оказывается справедливой и в случае, когда электромагнитная волна распространяется в диэлектрической или проводящей среде.

Поток Ф электромагнитной энергии через некоторую поверхность F можно найти с помощью интегрирования:

(4.3.18)

.

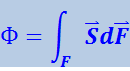С помощью формул (4.3.17) и (4.3.18) можно показать, что в замкнутой цепи постоянного тока энергия от участков, где действуют сторонние силы, передаётся другим участкам цепи не вдоль проводников, а через окружающее проводники пространство в виде потока электромагнитной энергии, характеризуемого вектором .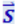

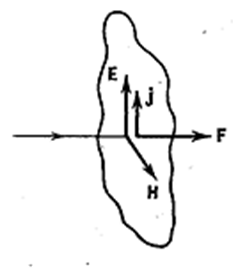
Поглощаясь в каком-либо теле, электромагнитная волна сообщает этому телу некоторый импульс, т.е. оказывает на него давление. Это можно показать на следующем примере. Пусть плоская волна падает по нормали на плоскую поверхность слабо проводящего тела с ε и μ, равными единице (рис. 4.3.3).

Электрическое поле волны возбудит в теле ток плотности . Магнитное поле волны будет действовать на ток с силой, величину которой в расчёте на единицу объёма тела можно найти по формуле

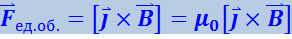
Направление этой силы, определяемое правилом левой руки, совпадает с направлением распространения волны.

Поверхностному слою с площадью, равной единице и толщиной dℓ сообщается в единицу времени импульс

(4.3.19)

.

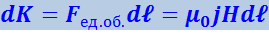В этом же слое в единицу времени поглощается энергия

(4.3.20)

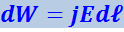
(необычность обозначения энергии и импульса обусловлена тем, что здесь наряду с этими понятиями используются напряжённость электрического поля и давление Р).

Найдём отношение импульса к энергии, разделив (4.3.19) на (4.3.20):

.

Приняв во внимание, что μ0H2 = ε0E2, получим:

.

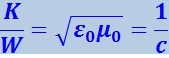Отсюда вытекает, что электромагнитная волна, несущая энергию W, обладает импульсом

(4.3.21)

.

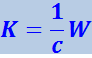Из (4.3.21) следует, что плотность импульса (т.е. импульс единицы объёма) электромагнитного поля равна

(4.3.22)

.

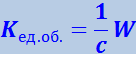Плотность энергии связана с модулем вектора Пойтинга соотношением S = ωc. Заменив в (4.3.21) ω через S/c и учтя, что направления векторов 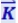и 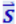совпадают, можно написать

(4.3.23)

.

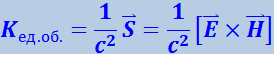Отметим, что при переносе любого вида энергии плотность потока энергии равна плотности импульса, умноженной на c2.

Пусть на некоторое тело падает нормально электромагнитная волна и полностью им поглощается. Тогда единице поверхности тела в единицу времени сообщается импульс волны, заключённый в цилиндре с площадью основания, равной единице, и высотой с. Согласно (4.3.22) этот импульс равен (ω/c) ⋅ c = ω. Вместе с тем импульс, сообщаемый единицей поверхности в единицу времени, равен давлению р на поверхность. Следовательно, в случае поглощающей поверхности p = ω. Эта величина пульсирует с большой частотой. Поэтому практически может быть измерено её среднее по времени значение. Таким образом,

(4.3.24)

.

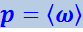Для идеально отражающей поверхности давление будет в два раза больше.

к к к