ФИЗИКА

4.3.2. Плоская электромагнитная волна

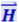Рассмотрим плоскую электромагнитную волну, распространяющуюся в нейтральной непроводящей среде с постоянными проницаемостями ε и μ (ρ = 0, j = 0, ε = const, μ = const). Направим ось х перпендикулярно к волновым поверхностям. Тогда и , а значит, и их компоненты по координатным осям не будут зависеть от координат y и z.

Можно показать, что дифференциальные уравнения, описывающие такую волну, будут выглядеть следующим образом:

(4.3.9)

,

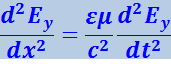(4.3.10)

.

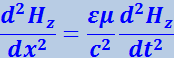Эти уравнения представляют собой частный случай уравнений (4.3.6) и (4.3.7).

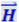Напомним, что Ex = Ez = 0 и Hx = Hy = 0, так что Ey = E и Hz = H. Мы сохранили в уравнениях (4.3.9) и (4.3.10) индексы y и z при Е и Н, чтобы подчеркнуть то обстоятельство, что и направлены вдоль взаимно перпендикулярных осей y и z.

Простейшим решением уравнения (4.3.9) является функция

(4.3.11)

.

Решение уравнения (4.3.10) имеет аналогичный вид

(4.3.12)

.

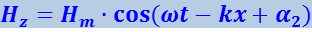В этих формулах ω - частота волны;

k - волновое число, равное ω/ν;

α1 и α2 - начальные фазы колебаний в точках с координатой x = 0.

Указанные решения удовлетворяют уравнениям (4.3.9) и (4.3.10), если α2 = α1, и

(4.3.13)

.

Умножив уравнение (4.3.11) на орт оси y, а уравнение (4.3.12) на орт оси z, получим уравнения плоской электромагнитной волны в векторном виде

(4.3.14)

(мы положили α2 = α1 = 0).

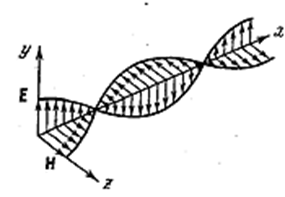
На рис. 4.3.1 показана «моментальная фотография» плоской электромагнитной волны. Из рисунка видно, что векторы и образуют с направлением распространения волны правовинтовую систему. В фиксированной точке пространства векторы и изменяются со временем по гармоническому закону. Они одновременно увеличиваются от нуля, а затем через 1/4 периода достигают наибольшего значения, причём, если направлен вверх, то 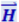направлен вправо (смотрим вдоль направления распространения волны). Ещё через 1/4 периода оба вектора одновременно обращаются в нуль. 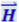Затем опять достигают наибольшего значения, но на этот раз направлен вниз, а влево. И, наконец, по завершении периода колебания векторы снова обращаются в нуль. Такие изменения векторов и происходят во всех точках пространства, но со сдвигом по фазе, определяемым расстоянием между точками, отсчитанным вдоль оси х.

к к к