ФИЗИКА

4.3.1. Волновое уравнение для электромагнитного поля

При рассмотрении электромагнитных явлений мы выясним, что переменное электрическое поле порождает магнитное, которое, вообще говоря, тоже оказывается переменным. Это переменное магнитное поле порождает электрическое и т.д. Таким образом, если возбудить с помощью колеблющихся зарядов переменное электромагнитное поле, то в окружающем заряды пространстве возникает последовательность взаимных превращений электрического и магнитного полей, распространяющихся от точки к точке. Этот процесс будет периодическим во времени и в пространстве и, следовательно, представляет собой волну.

Покажем, что существование электромагнитных волн вытекает из уравнений Максвелла. В случае однородной нейтральной (ρ = 0) непроводящей (j = 0) среды с постоянными проницаемостями ε и μ

.

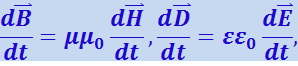
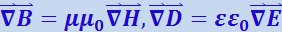Поэтому уравнения Максвелла можно написать следующим образом:

(4.3.1)

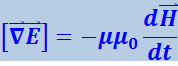
(4.3.2)

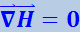
(4.3.3)

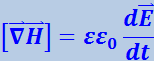
(4.3.4)

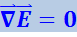
Возьмём ротор от обеих частей уравнения (4.3.1):

(4.3.5)

.

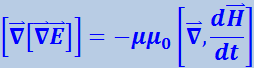Изменение последовательности дифференцирования по координатам и времени в правой части уравнения (4.3.5) приводит к равенству

.

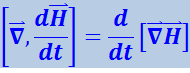Подставим этот результат в (4.3.5) и заменив в получившемся уравнении значение для ротора из уравнения (4.3.3), получим:

.

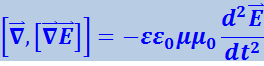. В силу (4.3.4) первый член этого выражения равен нулю. С учётом этого приходим к уравнению

.

Раскрыв оператор Лапласа, и учтя, что , будем иметь

(4.3.6)

.

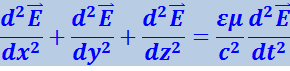Взяв ротор от обеих частей уравнения (4.3.3) и произведя аналогичные преобразования, придём к уравнению

(4.3.7)

.

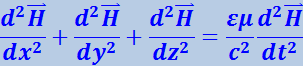Сравнив уравнения (4.3.6) и (4.3.7) с волновым, видим, что они тождественны друг другу. Значит, всякая функция, удовлетворяющая таким уравнениям, описывает некоторую волну, причём корень квадратный из величины, обратной коэффициенту при производной по времени, даёт фазовую скорость этой волны. Следовательно, уравнения (4.3.6) и (4.3.7) указывают на то, что электромагнитные поля могут существовать в виде электромагнитных волн, фазовая скорость которых равна

(4.3.8)

.

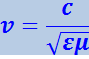В вакууме (т.е. при ε = μ = 1) скорость электромагнитных волн совпадает со скоростью света в пустоте с.

к к к