ФИЗИКА

4.2.8. Волновой пакет. Групповая скорость

Волна, имеющая форму короткого импульса (рис. 4.2.13), может быть представлена (интеграл Фурье) как суперпозиция (наложение) гармонических волн, частоты которых заключены в некотором интервале Δω.

Такое образование называется волновым пакетом или группой волн. В пределах пакета образующие его гармонические волны в большей или меньшей степени усиливают друг друга. Вне пакета эти волны практически гасят друг друга. Расчёт даёт, чем уже волновой пакет, тем больше должен быть интервал частот, представленных в пакете.

В отсутствие дисперсии все волны, образующие пакет, распространяются с одинаковой фазовой скоростью . Очевидно, что с такой же скоростью перемещается и волновой пакет, причём форма его не изменяется. В диспергирующей среде фазовая скорость гармонической волны зависит от частоты, поэтому пакет со временем расплывается – ширина его увеличивается. Если дисперсия невелика, расплывание пакета происходит не слишком быстро. В этом случае пакету можно приписать скорость U, под которой понимается скорость перемещения центра пакета, т.е. точки с максимальным значением амплитуды. Эту скорость называют групповой.

В диспергирующих средах групповая скорость оказывается отличной от фазовой. Покажем это на примере наложения двух волн с частотами и (соответственно с волновыми числами и ). Амплитуды волн будем считать одинаковыми. В этом случае уравнение волны имеет вид

.

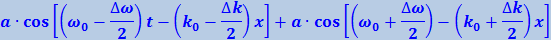Воспользовавшись формулой для суммы косинусов, преобразуем это уравнение следующим образом:

.

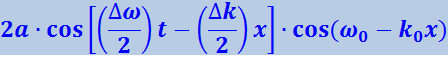Полученное уравнение можно рассматривать как уравнение бегущей гармонической волны с амплитудой, изменяющейся по закону

.

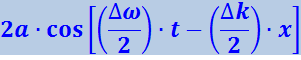Максимальное значение амплитуды получается при условии, что величина, стоящая под знаком косинуса, равна нулю. Отсюда следует, что координата xm центра волнового пакета в момент времени t определяется из соотношения

.

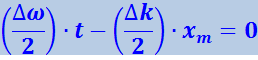Разделив xm на t, найдём скорость перемещения центра волнового пакета, т.е. групповую скорость:

.

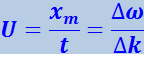В случае наложения волн с непрерывным набором частот групповая скорость определяется выражением

(4.2.52)

.

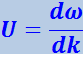Заменив согласно (4.2.10) ω через vk, выражение (4.2.52) можно представить в виде

(4.2.53)

.

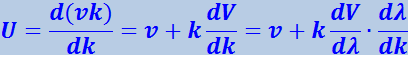По определению , т.е. . Следовательно, . Подстановка этого значения в (4.2.53) приводит к формуле

(4.2.54)

.

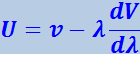В отсутствии дисперсии и .

Энергия волны пропорциональна квадрату амплитуды. Поэтому скорость переноса энергии волной равна групповой скорости. При значительном затухании волны понятие групповой скорости утрачивает смысл.

к к к