ФИЗИКА

4.2.7. Стоячие волны

Если в среде распространяется одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Значит, волны просто накладываются одна на другую, не возмущая друг друга. Это утверждение называется принципом суперпозиции волн.

В случае, когда колебания, обусловленные отдельными волнами в каждой из точек среды, обладают постоянной разностью фаз, волны называются когерентными. При сложении когерентных волн возникает явление интерференции, заключающееся в том, что колебания в одних точках усиливают, а в других точках ослабляют друг друга.

Важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой и частотой. Возникающий в результате колебательный процесс называется стоячей волной. Практически стоячие волны возникают при отражении волн от преград. Падающая на преграду волна и бегущая ей навстречу отражённая волна, налагаясь друг на друга, дают стоячую волну.

Напишем уравнения двух плоских волн, распространяющихся вдоль оси х в противоположных направлениях:

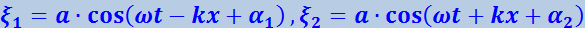
Сложив вместе эти уравнения и преобразовав результат по формуле для суммы косинусов, получим:

(4.2.43)

.

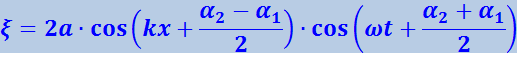Формула (4.2.42) – уравнение стоячей волны. Чтобы упростить его, выберем начало отсчёта х так, чтобы разность (α2 - α1) стала равной нулю, а начало отсчёта времени t – так, чтобы оказалась равной нулю сумма (α1 + α2). Кроме того, заменим . Тогда уравнение (4.2.43) примет вид

(4.2.44)

.

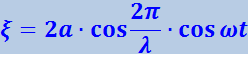Из (4.2.44) видно, что в каждой точке стоячей волны происходят колебания той же частоты, что и у встречных волн, причём амплитуда зависит от х

.

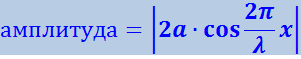В точках, координаты которых удовлетворяют условию

(4.2.45)

,

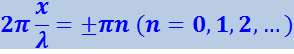амплитуда колебаний достигает максимального значения.

Эти точки называются пучностями стоячей волны. Из (4.2.45) получаются значения координат пучностей:

(4.2.46)

.

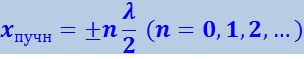В точках, координаты которых удовлетворяют условию

,

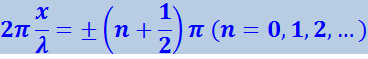амплитуда колебаний обращается в нуль.

Эти точки называются узлами стоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают. Координаты узлов имеют значения

(4.2.47)

.

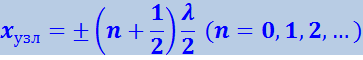Узел, как и пучность, представляет собой не одну точку, а плоскость, точки которой имеют значения координаты х, определяемые формулой (4.2.47).

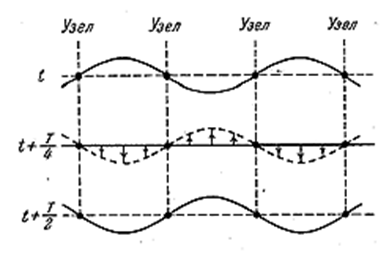
Из формул (4.2.46) и (4.2.47) следует, что расстояние между соседними пучностями, так же как и расстояние между соседними узлами, равно λ/2. Пучности и узлы сдвинуты друг относительно друга λ/4. Точки, лежащие по разные стороны от узла колеблются в противофазе, так как множитель в уравнении (4.2.44) при переходе через нулевое значение меняет знак. Все точки, заключённые между двумя соседними узлами, колеблются синфазно (т.е. в одинаковой фазе). На рис. 4.2.10 дан ряд «моментальных фотографий» отклонений точек от положения равновесия. Первая «фотография» соответствует моменту, когда отклонения достигают наибольшего абсолютного значения. Последующие «фотографии» сделаны с интервалами в четверть периода. Стрелками показаны скорости частиц.

Продифференцировав уравнение (4.2.44) один раз по t, а другой по х, найдём выражения для скорости частиц ξ и для деформации среды ε:

(4.2.48)

,

(4.2.49)

.

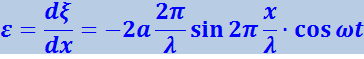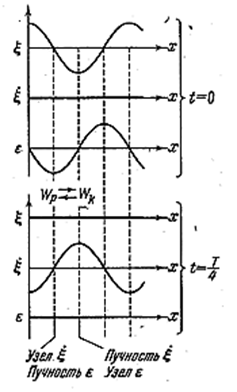
Эти уравнения описывают стоячую волну скорости (4.2.48) и стоячую волну деформации (4.2.49). На рис. (4.2.11) сопоставлены «моментальные фотографии» смещения, скорости и деформации для моментов времени 0 и T/4.

Из рисунка видно, что в то время, как ξ и ε достигают максимальных значений, ξ обращается в нуль и наоборот. Соответственно дважды за период происходит превращение энергии стоячей волны то полностью в потенциальную, сосредоточенную в основном вблизи узлов волны (где находятся пучности деформации), то полностью в кинетическую, сосредоточенную в основном вблизи пучностей волны (где находятся пучности скорости). В результате происходит переход энергии от каждого узла к соседним с ним пучностям и обратно. Средний по времени поток энергии в любом сечении волны равен нулю.

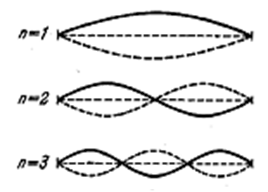
Колебания струны. В закреплённой с обоих концов натянутой струне при возбуждении поперечных колебаний устанавливаются стоячие волны, причём в местах закрепления струны должны располагаться узлы. Поэтому в струне возбуждаются с заметной интенсивностью только такие колебания, половина длины которых укладывается на длине струны целое число раз (рис. 4.2.12).

Отсюда вытекает условие

(4.2.50)

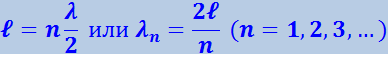
(ℓ − длина струны).

Длинам волн соответствуют частоты

(4.2.51)

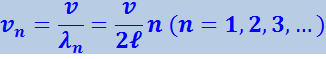
(ν – фазовая скорость волны, определяемая силой натяжения струны и массой единицы длины струны).

Частоты νn называются собственными частотами струны. Собственные частоты оказываются кратными частоте

,

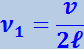которая называется основной частотой.

Гармонические колебания с частотами (4.2.51) называются собственными или нормальными колебаниями. В общем случае колебание струны представляет собой наложение различных гармоник.

Колебания струны примечательны в том отношении, что для них по классическим представлениям получаются дискретные значения одной из характеризующих колебания величин (частоты).

к к к