ФИЗИКА

4.2.5. Энергия упругой волны

Предположим, что в некоторой твёрдой среде распространяется в направлении оси х плоская продольная волна:

(4.2.25)

.

Выделим в среде элементарный объём ΔV настолько малый, чтобы скорость движения и деформацию во всех его точках можно было считать одинаковыми и равными соответственно и .

Выделенный объём обладает кинетической и потенциальной энергиями. Очевидно, что кинетическая энергия определяется соотношением

(4.2.26)

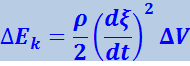
(ρ ⋅ ΔV - масса объёма; его скорость).

Нетрудно получить, что рассматриваемый объём обладает также потенциальной энергией упругой деформации

(4.2.27)

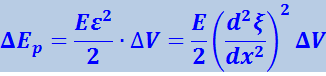
( - относительная деформация объёма; Е – модуль Юнга среды).

Заменим модуль Юнга, согласно (4.2.23) через ρν2. Тогда (4.2.27) примет вид:

(4.2.28)

.

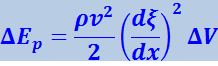Сумма выражений (4.2.26) и (4.2.28) даёт полную энергию объёма ΔV

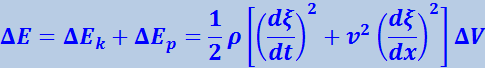
Разделив эту энергию на ΔV, получим плотность энергии:

(4.2.29)

.

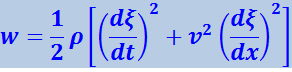Дифференцирование уравнения (4.2.25) один раз по t, другой раз по х даёт:

(4.2.30)

,

.

Подставив эти выражения в (4.2.29) и учтя, что k2ν2 = ω2, получим плотность энергии, возникающей в упругой среде при распространении в ней плоской продольной волны:

(4.2.31)

.

Можно показать, что для поперечной волны плотность энергии определяется такой же формулой. Выражение (4.2.30) справедливо для гармонических волн любого вида. Оно справедливо также и для затухающих волн.

Из (4.2.31) следует, что плотность энергии в каждый момент времени в разных точках пространства различна. В одной и той же точке плотность энергии изменяется со временем по закону квадрата синуса. Среднее значение квадрата синуса равно 1/2. Соответственно среднее по времени значение плотности энергии в данной точке среды равно

(4.2.32)

.

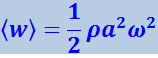Итак, среда, в которой распространяется упругая волна, обладает дополнительной механической энергией. Эта энергия доставляется от источника колебаний в различные точки среды самой волной. Количество энергии, переносимое волной через некоторую поверхность в единицу времени называется потоком энергии через эту поверхность. Если через поверхность за время dt энергия dE, то поток энергии Ф равен

(4.2.33)

.

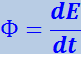Поток измеряется в ваттах.

Поток энергии в разных точках пространства может обладать различной интенсивностью. Для характеристики течения энергии в разных точках пространства используется векторная величина, называемая плотностью потока энергии. Эта величина численно равна потоку энергии через единичную площадку, помещённую в данной точке перпендикулярно к направлению, в котором переносится энергия. Направление вектора плотности потока энергии совпадает с направлением переноса энергии.

Модуль плотности потока энергии определяется выражением

.

Введя вектор, модуль которого равен фазовой скорости волны, а направление совпадает с направлением распространения волны, получим:

(4.2.34)

.

Этот вектор для упругих волн был введён Н.А. Умовым и называется вектором Умова. Он, вообще говоря, различен в разных точках пространства, а в данной точке изменяется со временем по закону квадрата синуса. Его среднее значение равно

(4.2.35)

.

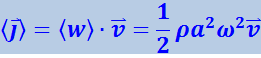Выражение (4.2.35) справедливо для волн любого вида.

Отметим, что под интенсивностью волны в данной точке подразумевается среднее по времени значение плотности потока энергии, переносимой волной.

Если известен вектор во всех точках произвольной поверхности S, можно по формуле

(4.2.36)

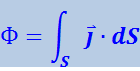
вычислить поток энергии через эту поверхность. Заменив в этой формуле вектор его средним по времени значением, получим среднее значение потока энергии:

(2.37)

.

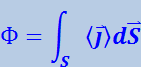Найдём среднее значение потока энергии через одну из волновых поверхностей незатухающей сферической волны. В каждой точке этой поверхности векторы и совпадают по направлению. Кроме того, модуль вектора для всех точек поверхности одинаков. Следовательно,

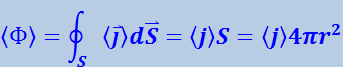
(r – радиус волновой поверхности).

Согласно (4.2.35) . Поэтому

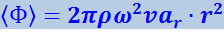
(ar - амплитуда волны на расстоянии r от источника).

Поскольку энергия волны не поглощается средой, средний поток энергии через сферу любого радиуса должен иметь одинаковое значение, т.е. должно выполняться условие:

.

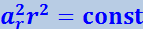Отсюда следует, что амплитуда ar незатухающей сферической волны обратна расстоянию r от источника. Соответственно средняя плотность потока энергии ⟨j⟩, т.е. интенсивность волны, обратно пропорциональна квадрату расстояния от источника.

к к к