ФИЗИКА

4.2.4. Скорость упругих волн в твёрдой среде

Рассмотрим цилиндрический стержень из однородного и изотропного материала. Допустим, что вдоль стержня распространяется плоская гармоническая волна. В этом случае частицы, лежащие в поперечном сечении стержня, определяемой координатой х, будут претерпевать смещение ξ, описываемое уравнением

(4.2.19)

.

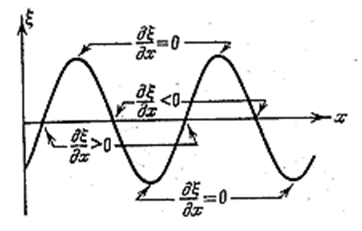
График этой функции дан на рис. 4.2.5.

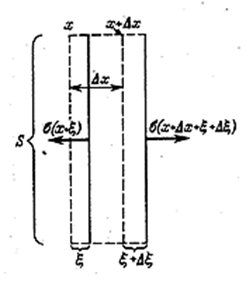
Выделим в стержне элемент длины Δx, ограниченный в отсутствие волны сечениями х и x + Δx (рис. 4.2.6).

Если сечение с координатой х имеет в некоторый момент времени смещение ξ, то смещение сечения с координатой x + Δx будет .

Поскольку смещения сечений с разными значениями координаты х неодинаковы, рассматриваемый элемент стержня оказывается деформированным – он получает удлинение . Отношение даёт среднее значение ⟨ε⟩ относительного удлинения стержня Δx. Чтобы получить деформацию ε в сечении х, нужно устремить Δx к нулю. Следовательно,

(4.2.20)

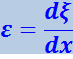
(символ частной производной взят потому, что ξ зависит не только от х, но и от t).

Наличие деформации растяжения свидетельствует о существовании в сечении х нормального напряжения σ

(4.2.21)

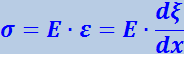
(Е – модуль Юнга материала стержня).

Относительная деформация , а, следовательно, и напряжение σ в фиксированный момент времени зависят от х (рис. 4.2.5). Там, где смещения сечений от положения равновесия максимальны, деформация и напряжение равны нулю. В местах, где сечения проходят через положения равновесия, деформация и напряжение достигают наибольшего значения, причём положительная и отрицательная деформации (т.е. растяжения и сжатия) чередуются друг с другом. В соответствии с этим продольная волна состоит из чередующихся растяжений и сжатий среды.

Написав для изображённого на рис. 4.2.6 элемента стержня второй закон Ньютона, после преобразований придём к волновому уравнению

(4.2.22)

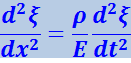
(ρ - плотность недеформированного стержня).

Сравнение уравнений (4.2.22) и (4.2.17) даёт для фазовой скорости продольной упругой волны в стержне выражение

(4.2.23)

.

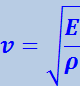Аналогичные вычисления для поперечных волн приводят к формуле

(4.2.24)

,

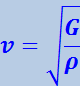где G – модуль сдвига.

к к к