ФИЗИКА
Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Чтобы установить вид волнового уравнения, сопоставим вторые частные производные по координатам и времени от функции (4.2.13), описывающей плоскую волну. Продифференцировав эту функцию дважды по каждой из переменных, получим:
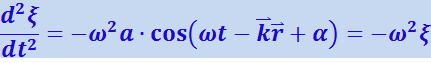
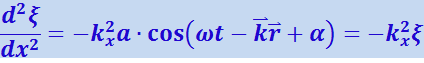
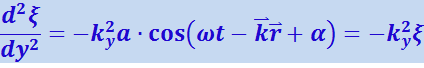
Сложение производных по координатам даёт
(4.2.16)
.
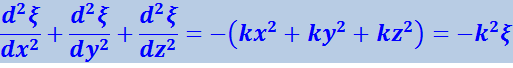Сопоставив эту сумму с производной по времени и заменив k2/ω2 через 1/ν2, получим уравнение
(4.2.17)
.
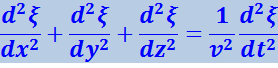Это и есть волновое уравнение. Его можно записать в виде
(4.2.18)
,
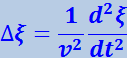где Δ - оператор Лапласа.
Всякая функция, удовлетворяющая уравнению вида (4.2.17), описывает некоторую волну, причём корень квадратный из величины обратной коэффициенту при 
, даёт фазовую скорость этой волны.
к к к