ФИЗИКА

4.2.2. Уравнение плоской и сферической волн

Уравнением волны называется выражение, которое даёт смещение колеблющейся частицы как функцию её координат x, y, z и времени t.

(4.2.3)

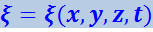
(имеются в виду координаты равновесного положения частицы).

Эта функция должна быть периодической как относительно времени t, так и относительно координат x, y, z. Периодичность по координатам следует из того, что точки, отстоящие друг от друга на расстояние λ , колеблются одинаковым образом.

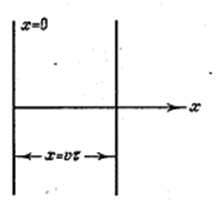
Найдём вид функции ξ в случае плоской волны, полагая, что колебания носят гармонический характер. Для упрощения направим оси координат так, чтобы ось х совпала с направлением распространения волны. Тогда волновые поверхности будут перпендикулярными к оси х и, поскольку все точки волновой поверхности колеблются одинаково, смещение ξ будет зависеть только от х и t : . Пусть колебания точек, лежащих в плоскости x = 0 (рис. 4.2.4), имеют вид

.

Найдём вид колебания точек в плоскости, соответствующей значению х. Для того, чтобы пройти путь от плоскости x = 0 до этой плоскости, волне требуется время (ν - скорость распространения волны). Следовательно, колебания частиц, лежащих в плоскости х, будут отставать по времени на τ от колебаний частиц в плоскости x = 0, т.е. будут иметь вид

(4.2.4)

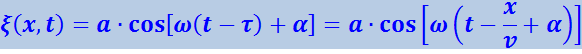
Итак, уравнение плоской волны (и продольной и поперечной), распространяющейся в направлении оси х, выглядит следующим образом:

(4.2.5)

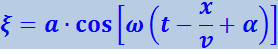
Величина α представляет собой амплитуду волны. Начальная фаза волны α определяется выбором начал отсчёта х и t.

Зафиксируем некоторое значение фазы в уравнении (4.2.5), положив

(4.2.6)

.

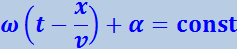Это выражение определяет связь между временем t и тем местом х, в котором фаза имеет зафиксированное значение. Вытекающее из него значение даёт скорость, с которой перемещается данное значение фазы. Продифференцировав (4.2.6), получим:

,

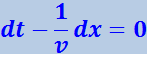откуда

(4.2.7)

.

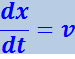Таким образом, скорость распространения волны v в уравнении (4.2.5) есть скорость перемещения фазы, в связи с чем её называют фазовой скоростью.

Согласно (4.2.7) . Следовательно, уравнение (4.2.5) описывает волну, распространяющуюся в противоположном направлении, описывается уравнением

(4.2.8)

.

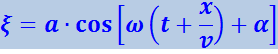Действительно, прировняв константе фазу волны (4.2.8) и продифференцировав получившееся равенство, придём к соотношению

,

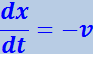из которого следует, что волна (4.2.8) распространяется в сторону убывания х.

Уравнению плоской волны можно придать симметричный относительно х и t вид. Для этого введём величину

(4.2.9)

,

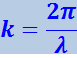которая называется волновым числом. Умножив числитель и знаменатель выражения (4.2.9) на частоту ν, можно представить волновое число в виде

(4.2.10)

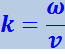
Раскрыв в (4.2.5) круглые скобки и приняв во внимание (4.2.10), придём к следующему уравнению плоской волны, распространяющейся вдоль оси х:

(4.2.11)

.

Уравнение волны, распространяющейся в сторону убывания х, отличается от (4.2.11) только знаком при члене kx.

Если направление распространения плоской волны образует с осями координат x, y, z углы α, β, γ, отличные от нуля, то можно показать, что уравнение волны будет выглядеть следующим образом:

(4.2.12)

,

где - волновой вектор, равный по модулю волновому числу и направленный по нормали к волновой поверхности.

Функция (4.2.12) даёт смещение из положения равновесия точки с радиус-вектором в момент времени t ( определяет равновесное положение точки). Чтобы перейти от радиус-вектора точки к её координатам x, y, z, выразим скалярное произведение через компоненты векторов по координатным осям:

.

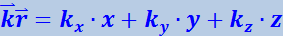Тогда уравнение плоской волны примет вид

(4.2.13)

.

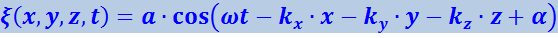Здесь

(4.2.14)

.

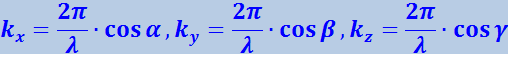При выводе формулы (4.2.11) мы полагали, что амплитуда колебаний не зависит от х. Для плоской волны это наблюдается, когда энергия волны не поглощается средой. При распространении волны в поглощающей среде интенсивность волны с удалением от источника колебаний уменьшается.

Теперь найдём уравнение сферической волны. Всякий реальный источник волн обладает некоторой протяжённостью. Однако, если ограничиться рассмотрением волны на расстояниях от источника, значительно превышающих его размеры, то источник можно считать точечным. В однородно и изотропной среде волна, порождаемая точечным источником, будет сферической.

Допустим, что фаза колебаний источника равна (ωt + a). Тогда точки, лежащие на волновой поверхности радиуса r, будут колебаться с фазой

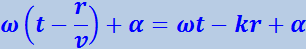
(чтобы пройти путь r, волне требуется время ).

В силу того, что волны сферические, амплитуда колебаний при отсутствии поглощения энергии убывает с расстоянием от источника по закону 1/r. Следовательно, уравнение сферической волны имеет вид:

(4.2.15)

,

где α – постоянная величина, численно равная амплитуде на расстоянии от источника, равном единице. Отметим, что при стремлении r к нулю выражение для амплитуды обращается в бесконечность. Этот результат объясняется неприменимостью уравнения для малых r.

к к к