ФИЗИКА

4.2.1. Распространение волн в упругой среде

Если в каком-либо месте упругой среды возбудить колебания её частиц, то вследствие взаимодействия между частицами это колебание будет распространяться в среде от частицы к частице с некоторой скоростью v. Процесс распространения колебаний в пространстве называется волной.

Волны могут иметь различную форму. Одиночной волной или импульсом называется короткое возмущение, не имеющее регулярного характера (рис. 4.2.1а). Ограниченный ряд повторяющихся возмущений называется цугом волн. Обычно под цугом понимают отрезок синусоиды (рис. 4.2.1б). Особое значение в теории волн имеет гармоническая волна, т.е. бесконечная синусоидальная волна (рис. 4.2.1в).

Мы начнём с рассмотрения упругих гармонических волн.

Отметим, что частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. Упругие поперечные волны могут возникать лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твёрдой среде возможно возникновение как продольных, так и поперечных волн.

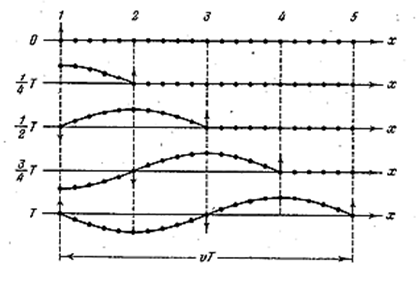
На рис. 4.2.2 показано движение частиц при распространении в среде поперечной волны. Номерами 1,2 и т.д. обозначены частицы, отстоящие друг от друга на расстояние, равное , т.е. на расстояние, проходимое волной за четверть периода колебаний, совершаемых частицами. В момент времени, принятый за нулевой, волна, распространяясь вдоль оси слева направо достигла частицы 1, вследствие чего частица начала смещаться из положения равновесия вверх, увлекая за собой следующие частицы. Спустя четверть периода частица 1 достигает крайнего верхнего положения; одновременно начинает смещаться из положения равновесия частица 2. По прошествии ещё четверти периода первая частица будет проходить положение равновесия, двигаясь в направлении сверху вниз, вторая частица достигнет крайнего верхнего положения, а третья частица начнёт смещаться вверх из положения равновесия. В момент времени, равный Т, первая частица закончит полный цикл колебания и будет находиться в таком же состоянии движения, как и в начальный момент. Волна к моменту времени Т, пройдя путь vT, достигнет частицы 5.

Все рассуждения, касающиеся поведения частиц в поперечной волне, могут быть отнесены и к продольной волне. В ней в направлении распространения волны перемещаются сгущения и разрежения частиц.

На рис. 4.2.2 показаны колебания частиц, положения равновесия которых лежат на оси х. В действительности колеблются не только частицы, расположенные вдоль оси х, а совокупность частиц в некотором объёме.

Распространяясь от источника колебаний, волновой процесс охватывает всё новые и новые части пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны.

Фронт волны отделяет часть пространства, уже вовлечённую в волновой процесс, от области, в которой колебания ещё не возникли.

Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновых поверхностей существует бесконечное множество, в то время как волновой фронт в каждый момент времени только один.

Волновые поверхности могут быть любой формы. В частности, они могут иметь форму плоскости и сферы. Соответственно волна в этих случаях называется плоской или сферической. Именно такие волны мы и будем рассматривать ниже.

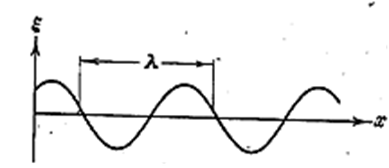
Пусть плоская волна распространяется вдоль оси х. Тогда все точки среды, положения равновесия которых имеют одинаковую координату х (но различные значения координат y и z), колеблются в одинаковой фазе. На рис. 4.2.3 изображена кривая, которая даёт смещение ξ из положения равновесия точек с различными х в некоторый момент времени.

Расстояние λ, на которую распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны.

(4.2.1)

,

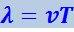где ν – скорость волны;

Т – период колебаний.

Заменив Т через 1/ν (ν – частота колебаний), получим:

(4.2.2)

.

к к к