ФИЗИКА

4.1.10. Переменный ток

Установившиеся вынужденные колебания можно рассматривать как протекание в цепи, обладающей ёмкостью, индуктивностью и активным сопротивлением, переменного тока, обусловленного переменным напряжением

(4.1.119)

.

Согласно (4.1.107) этот ток изменяется по закону

(4.1.120)

.

Амплитуда тока определяется амплитудой напряжения Um, параметрами цепи L, C, R и частотой ω:

(4.1.121)

.

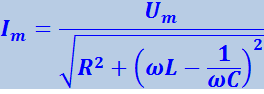Ток отстаёт по фазе от напряжения на угол φ:

(4.1.122)

.

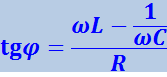Стоящее в формуле (4.1.121) выражение

(4.1.123)

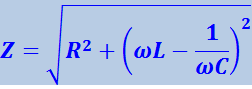
называется полным электрическим сопротивлением или импедансом.

Если цепь состоит из одного лишь активного сопротивления R, уравнение закона Ома имеет вид

.

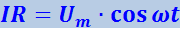Из этой формулы следует, что ток в этом случае изменяется в фазе с напряжением, а амплитуда силы тока равна

.

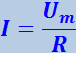Всякая реальная цепь обладает R, L и C. В отдельных случаях некоторые из этих параметров бывают таковы, что их влиянием на ток можно пренебречь. Допустим, что R цепи можно положить равным нулю, а С – равным бесконечности. Тогда из формул (4.1.121) и (4.1.122) следует, что

(4.1.124)

,

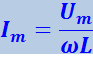а tgφ = ∞ (соответственно ).

Величину

(4.1.125)

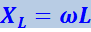
называют реактивным индуктивным сопротивлением или просто индуктивным сопротивлением цепи.

Если L выразить в генри, а ω - в , XL будет выражено в омах. Индуктивное сопротивление растёт с частотой (4.1.125).

Постоянному току (ω = 0) индуктивность не оказывает сопротивления.

Теперь допустим, что можно положить равными нулю R и L. Тогда согласно (4.1.121) и (4.1.122)

(4.1.126)

,

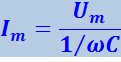а  tgφ = -∞ (т.е. ).

Величину

(4.1.127)

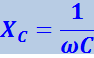
называют реактивным ёмкостным сопротивление или ёмкостным сопротивлением.

Если С выразить в фарадах, а ω - в , то XC будет выражено в омах.

Из (4.1.126) следует, что ёмкостное сопротивление убывает с частотой. Для постоянного тока XC = ∞ - постоянный ток через конденсатор течь не может. Ток, текущий через конденсатор, опережает напряжение на π/2.

Наконец, допустим, что можно положить R равным нулю. В этом случае согласно (4.1.121)

(4.1.128)

.

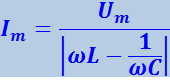(4.1.129)

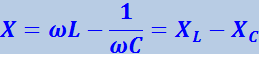
называется реактивным сопротивлением или реактансом.

Формулы (4.1.122) и (4.1.123) можно представить в виде

.

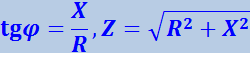Таким образом, если значения сопротивлений R и Х отложить вдоль катетов треугольника, то длина гипотенузы будет численно равна Z (рис. 4.1.25а).

Найдём мощность, выделяемую в цепи переменного тока. Мгновенное значение мощности равно произведению мгновенных значений напряжения и силы тока

(4.1.130)

Практический интерес представляет среднее по времени значение мощности Р. Так как среднее значение cos(2ωt - φ) равно нулю,

(4.1.131)

.

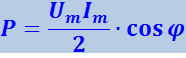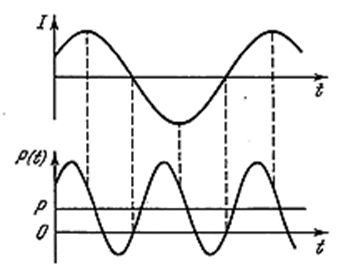
Из (4.1.130) следует, что мгновенная мощность колеблется около среднего значения с частотой, в два раза превышающей частоту тока (рис. 4.1.27).

В соответствии с диаграммой рис. 4.1.27

.

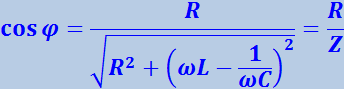Подставив это значение cosφ в формулу (4.1.131) и учтя, что Um/Z = Im, получим

(4.1.132)

.

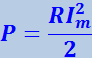Такую же мощность развивает постоянный ток, сила которого равна

(4.1.133)

.

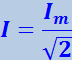Величина (4.1.133) называется действующим (или эффективным) значением силы тока. Аналогично величина

(4.1.134)

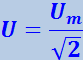
называется действующим значением напряжения.

Выражение средней мощности через действующие значения силы тока и напряжения имеет вид:

(4.1.135)

.

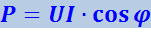Входящий в это выражение множитель cosφ называют коэффициентом мощности. В технике стремятся сделать cosφ как можно бόльшим.

к к к