ФИЗИКА

4.1.9. Вынужденные электрические колебания

Вынужденные электрические колебания в последовательном образовавшиеся контакты переменное напряжение

(4.1.100)

.

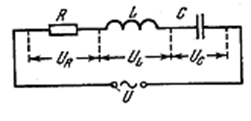
Запишем закон Ома для цепи, изображённой на рис. 4.1.24:

(4.1.101)

.

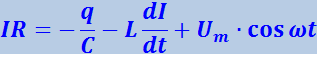Разделив это уравнение на L и заменив I через , а через , получим:

(4.1.102)

.

Принимая во внимание, что и , будем иметь

(4.1.103)

.

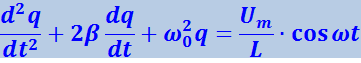Уравнение (4.1.103) совпадает с дифференциальным уравнением вынужденных механических колебаний (4.1.87). Частное решение этого уравнения имеет вид:

(4.1.104)

,

где

.

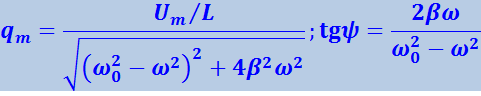Подстановка в эти формулы значений ω02 и β даёт

(4.1.105)

;

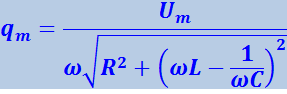(4.1.106)

.

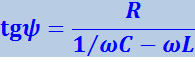Общее решение получится, если к частному решению (4.1.104) прибавить общее решение соответствующего однородного уравнения. Это решение получено при рассмотрении затухающих колебаний (4.1.77); оно содержит экспоненциальный множитель e-βt, поэтому по прошествии достаточного времени им можно пренебречь. Следовательно, установившиеся вынужденные колебания описываются функцией (4.1.104).

Продифференцировав выражение (1.104) по t, найдём силу тока в контуре при установившихся колебаниях:

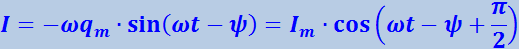
(Im = ωqm).

Запишем полученное выражение в виде

(4.1.107)

,

где есть сдвиг по фазе между током и напряжением.

В соответствии с (4.1.106)

(4.1.108)

.

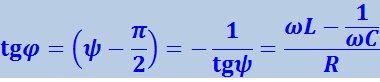Из этой формулы следует, что ток отстаёт по фазе от напряжения (φ > 0), если , и опережает напряжение (φ < 0) при условии, что .

Из (4.1.105) следует, что

(4.1.109)

.

Представим (4.1.102) в виде

(4.1.110)

.

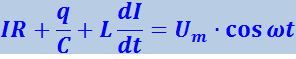Произведение IR равно напряжению UR на активном сопротивлении;

- напряжение на конденсаторе UC;

определяет напряжение на индуктивности UL.

С учётом этого можно написать

(4.1.111)

.

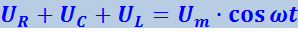Таким образом, сумма напряжений на отдельных элементах контура равна в каждый момент времени напряжению, приложенному извне.

В соответствии с (4.1.107)

(4.1.112)

.

Разделив (4.1.104) на ёмкость, получим напряжение на конденсаторе

(4.1.113)

.

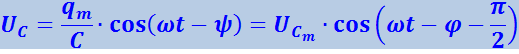Здесь

(4.1.114)

.

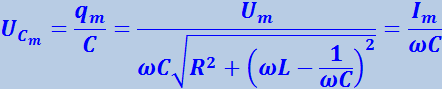Умножив производную функции (4.1.107) на L, получим напряжение на индуктивности:

(4.1.115)

.

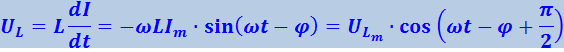Здесь

(4.1.116)

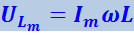
Сопоставление формул (4.1.107), (4.1.112), (4.1.113) и (4.1.115) показывает, что напряжение на ёмкости отстаёт по фазе от силы тока на π/2, а напряжение на индуктивности опережает ток на π/2. Напряжение на активном сопротивлении изменяется в фазе с током.

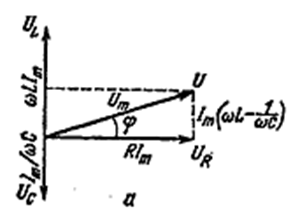
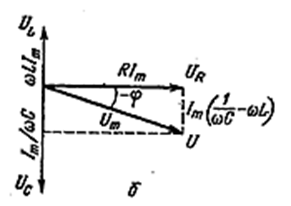
На рис. 4.1.25 приведены векторные диаграммы вынужденных колебаний в электрическом контуре для трёх случаев. За основную принята ось тока. Поэтому UR изображено вектором, направленным вправо по горизонтали. Сумма векторов UR, UL и UC равна вектору U, изображающему напряжение, приложенное к контуру.

На рис. 4.1.25б показана диаграмма для случая, когда , т.е. ω < ω0. В случае б угол φ отрицателен (он отложен по часовой стрелке); на рисунке указано абсолютное значение угла, равное -φ.

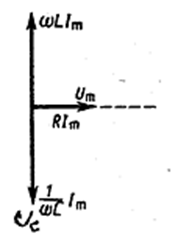
Из диаграмм на рис. 4.1.25 а и б видно, что, когда ω > ω0, ток отстаёт по фазе от приложенного напряжения, а при ω < ω0 ток опережает напряжение. Если ω = ω0, а значит ωL = 1 / ωC, фазы тока и приложенного напряжения совпадают (рис. 4.1.25в).

В этом случае знаменатель в (4.1.109) становится минимальным, ток Im - максимальным и при данном Um определяется только активным сопротивлением R. Падение напряжения на R равно внешнему напряжению, приложенному к цепи, а напряжения на конденсаторе и катушке одинаковые по амплитуде и противоположны по фазе. Это явление называется резонансом напряжений.

Резонансная частота для заряда q и напряжения на конденсаторе UC равна

(4.1.117)

.

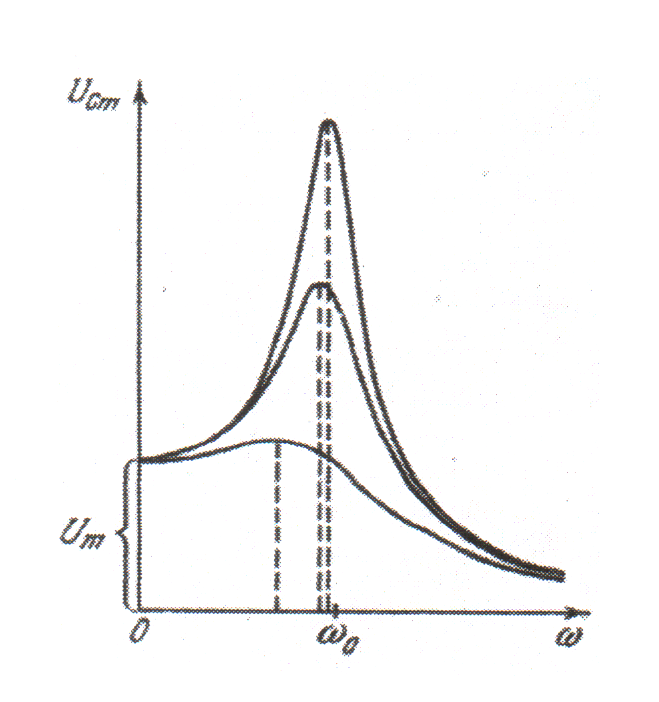
Резонансные кривые для UC изображены на рис. 4.1.26. Они подобны резонансным кривым для механических колебаний (см. рис. 4.1.22).

При ω → 0 кривые сходятся в одной точке с ординатой UCm, равной напряжению, возникающему на конденсаторе при подключении его к источнику постоянного напряжения Um. Максимум при резонансе получается тем выше и острее, чем меньше , т.е. чем меньше активное сопротивление и больше индуктивность контура.

Из формулы (4.1.109) следует, что амплитуда силы тока Im достигает максимума при . Отсюда для резонансной частоты тока получается значение

.

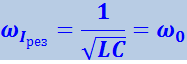Таким образом, резонансная частота для силы тока совпадает с собственной частотой контура.

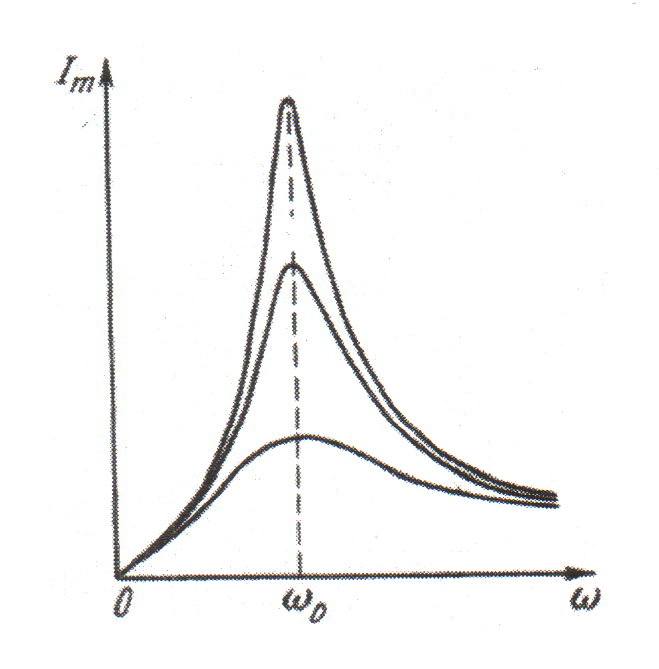
Резонансные кривые для силы тока изображены на рис. 4.1.27. По виду они совпадают с резонансными кривыми для скорости механических вынужденных колебаний. При стремлении частоты к нулю амплитуда силы тока также стремится к нулю – постоянный ток в цепи с конденсатором течь не может.

При малом затухании (β2 << ω02) резонансную частоту для напряжения можно положить равной ω0. Соответственно будет равно нулю. Согласно (4.1.114) для отношения амплитуды напряжения на конденсаторе при резонансе UCmрез. К амплитуде внешнего напряжения Um в этом случае получается значение

(4.1.118)

.

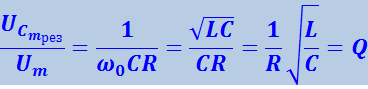Таким образом, добротность контура показывает, во сколько раз напряжение на конденсаторе может превысить приложенное напряжение.

Явление резонанса используется для выделения из сложного напряжения нужной составляющей. Пусть напряжение, приложенное к контуру равно

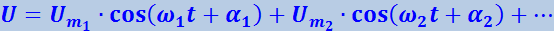
Настроив контур на одну из частот ω1, ω2 и т.д., можно получить на конденсаторе напряжение в Q раз превышающее значение данной составляющей, в то время как напряжение, создаваемое на конденсаторе другими составляющими, будет слабым. Такой процесс осуществляется, например, при настройке радиоприёмника на нужную длину волны.

к к к