ФИЗИКА

4.1.8. Вынужденные колебания

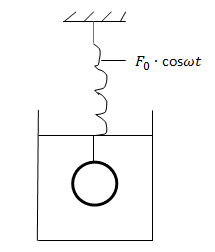
Начнём с механических колебаний и рассмотрим их на примере пружинного маятника. Допустим, что на шарик массой т, опущенный в сосуд с глицерином, действует внешняя сила, изменяющаяся по закону F0 ⋅ cosωt, где ω - частота силы.

Для установления характера движения шарика запишем второй закон Ньютона:

(4.1.86)

.

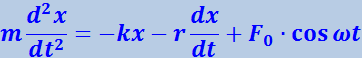Разделим уравнение (4.1.86) на т и введём обозначения , . Тогда получим:

(4.1.87)

.

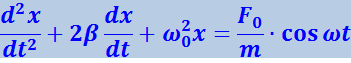Здесь β - коэффициент затухания;

ω0 - собственная частота системы;

F0 - амплитуда вынуждающей силы.

Уравнение (4.1.87) является неоднородным. Общее решение такого уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения. Общее решение однородного уравнения мы уже знаем (см. затухающие колебания). Оно имеет вид:

(4.1.88)

,

где ,

a0 и L - произвольные постоянные.

Остаётся найти частное. Получим его с помощью векторной диаграммы. Предположим, что частное решение уравнения (4.1.87) имеет вид:

(4.1.89)

.

Тогда

(4.1.90)

,

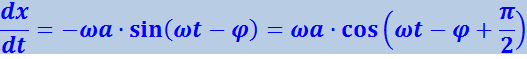(4.1.91)

.

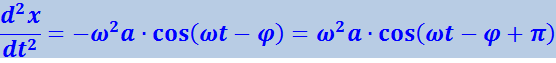Подстановка выражений (4.1.89) – (4.1.91) в уравнение (4.1.87) приводит к соотношению

(4.1.92)

.

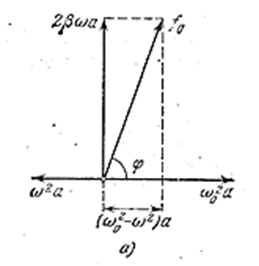
Из (4.1.92) следует, что постоянные а и φ должны иметь такие значения, чтобы гармоническая функция была равна сумме трёх гармонических функций, стоящих в левой части уравнения. Если изобразить функцию ω02a ⋅ cos(ωt - φ) вектором длины ω02a, направленным вправо, то функция вектором длины 2βωa (рис. 4.1.20), повёрнутым относительно ω2a против часовой стрелки на угол π/2, а функция ω2a ⋅ cos(ωt - φ + π) - вектором длины ω2a, повёрнутым относительно вектора ω2a против часовой стрелки на угол π. Чтобы уравнение (4.1.92) было удовлетворено, сумма трёх перечисленных векторов должна совпадать с вектором, изображающим функцию .

Из рис. 4.1.20а видно, что такое совпадение возможно лишь при значении амплитуды а, которое определяется условием:

,

откуда

(4.1.93)

.

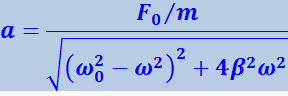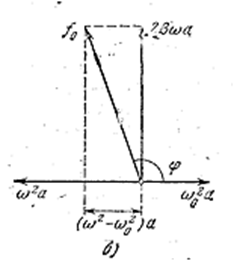
Рис. 4.1.20а отвечает случаю ω < ω0. Из рис. 4.1.20б, отвечающего случаю ω > ω0, получается такое же значение а.

Рис. 4.1.20 позволяет получить также и значение φ, которое представляет собой величину отставания по фазе вынужденного колебания (4.1.89) от обусловившей его вынужденной силы. Из рисунка следует, что

(4.1.94)

.

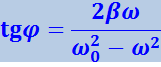Подставив в (4.1.89) значения а и φ, определяемые формулами (4.1.93) и (4.1.94), получим:

(4.1.95)

.

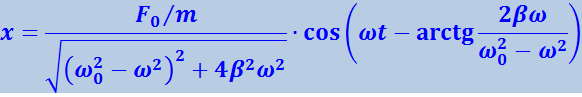Функция (4.1.95) в сумме с (4.1.88) даёт общее решение уравнения (4.1.87), описывающее поведение системы при вынужденных колебаниях. Слагаемое (4.1.87) играет заметную роль только в начальной стадии процесса при установлении колебаний.

С течением времени из-за экспоненциального множителя e-βt роль слагаемого (4.1.88) всё больше уменьшается, и по прошествии достаточного времени им можно пренебречь, сохраняя в решении лишь слагаемое (4.1.95).

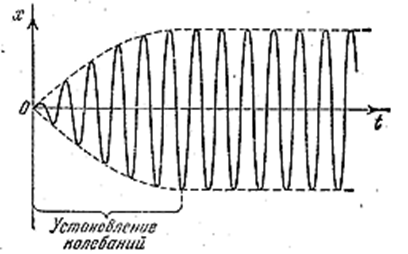
Таким образом, функция (4.1.95) описывает установившиеся вынужденные колебания. Они представляют собой гармонические колебания с частотой, равной частоте вынуждающей силы. Амплитуда (4.1.93) вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Для данной колебательной системы (определённых ω0 и β) амплитуда зависит от частоты вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причём величина отставания φ также зависит от частоты вынуждающей силы (4.1.94).

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определённой для данной системы частоте амплитуда достигает максимального значения. Это явление называется резонансом, а соответствующая частота – резонансной частотой.

Чтобы определить резонансную частоту ωрез., нужно найти максимум функции (4.1.93) или, что то же самое, минимум выражения, стоящего под корнем в знаменателе. Продифференцировав это выражение по ω и приравняв к нулю, мы получим условие, определяющее ωрез.:

(4.1.96)

.

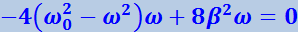Уравнение (4.1.96) имеет три решения: и . Решение, равное нулю, соответствует максимуму знаменателя. Из остальных двух решений отрицательное должно быть отброшено, как не имеющее физического смысла (частота не может быть отрицательной). Таким образом, для резонансной частоты получается одно значение:

(4.1.97)

.

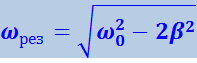Подставив это значение частоты в (4.1.93), получим выражение для амплитуды при резонансе

(4.1.98)

.

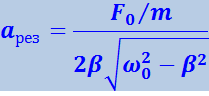Из (4.1.98) следует, что при отсутствии сопротивления среды амплитуда при резонансе обращалась бы в бесконечность. Согласно (4.1.97) резонансная частота при тех же условиях (β = 0) совпадает с собственной частотой колебаний системы ω0.

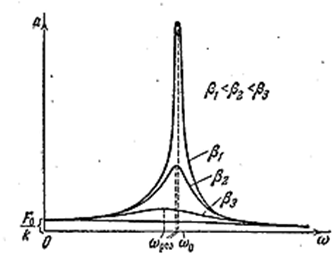
Зависимость амплитуды вынужденных колебаний от частоты показана на рис. 4.1.22. Отдельные кривые на графике соответствуют различным значениям параметра β. Чем меньше β, тем выше и правее лежит максимум данной кривой. При очень большом затухании (2β2 > ω02) выражение для резонансной частоты становится мнимым. Это означает, что при этих условиях резонанс не наблюдается. Изображённая на рис. 4.1.22 совокупность графиков называется резонансными кривыми.

По поводу резонансных кривых можно сделать ещё следующие замечания. При стремлении ω к нулю все кривые приходят к одному и тому же значению, равному F0/mω02 = F0/k. Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы величины F0. При стремлении ω к бесконечности все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет своё направление, что система не успевает заметно сместиться из положения равновесия. Наконец, отметим, что чем меньше β, тем сильнее изменяется с частотой амплитуда вблизи резонанса, тем «острее» получается максимум.

Из формулы (4.1.98) вытекает, что при малом затухании (т.е. при β << ω0) амплитуда при резонансе приближённо равна

.

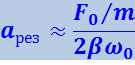Разделим это выражение на смещение x0 от положения равновесия под действием постоянной силы F0, равное F0/mω02. В результате получим:

(4.1.99)

.

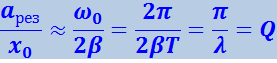Таким образом, добротность Q показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы (это справедливо лишь при малом затухании).

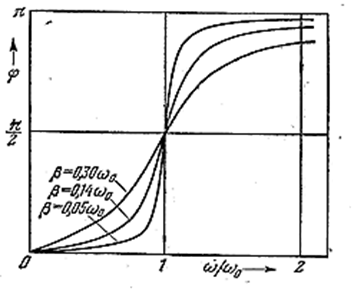
Из рис. 4.1.20 видно, что вынужденные колебания отстают по фазе от вынуждающей силы, причём величина отставания φ лежит в пределах от 0 до π. Зависимость φ от ω при разных значениях β показана на рис. 4.1.23. Частоте ω0 соответствует φ = π/2.

С явлением резонанса приходится считаться. Так, например, собственная частота вибраций корпуса корабля или крыльев самолёта должна сильно отличаться от частоты колебаний, которые могут быть возбуждены вращением гребного винта или пропеллера.

Вместе с тем явление резонанса оказывается полезным особенно в радиотехнике, акустике и т.д.

к к к