ФИЗИКА
Начнём с механических. Опустим шарик пружинного маятника (рис. 4.1.1) в сосуд, например, с глицерином. В этом случае в процессе колебаний на шарик будет действовать не только квазиупругая сила, но и сила сопротивления 
cо стороны жидкости. При малых колебаниях силу сопротивления можно считать пропорциональной величине скорости шарика:
(4.1.60)
.
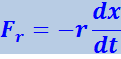Здесь r – постоянная, называемая коэффициентом сопротивления. Знак минус обусловлен тем, что сила 
и скорость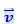 
имеют противоположные направления; следовательно, их проекции на ось х имеют разные знаки.
Чтобы определить характер движения шарика в этом случае, запишем второй закон Ньютон
(4.1.61)
.
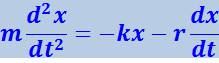Преобразуем уравнение (4.1.61), введя обозначения
(4.1.62)
,
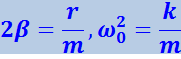где β - коэффициент затухания;
ω0 - частота, с которой совершались бы свободные колебания системы в отсутствии сопротивления среды (при r = 0).
С учётом (4.1.62) получим:
(4.1.63)
.
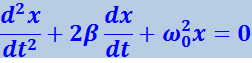Это дифференциальное уравнение описывает затухающие колебания пружинного маятника. Оно же, как будет показано ниже, описывает затухающие колебания любой другой системы независимо от природы колеблющейся величины.
При не слишком сильном затухании решение уравнения (4.1.63) имеет вид:
(4.1.64)
.
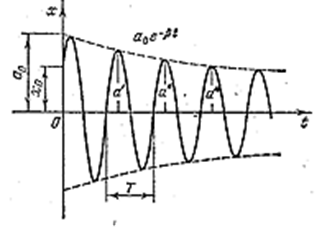
Здесь а0 и α - произвольные постоянные; 
- частота затухающих колебаний. На рис. 4.1.16 представлен график функции (4.1.64). Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки х.
Рис. 4.1.16 |
В соответствии с видом функции (4.1.64) движение шарика можно рассматривать как колебание частоты ω с амплитудой, изменяющейся по закону 
.
Верхняя из пунктирных кривых на рис. 4.1.16 даёт график функции 
, причём величина a0 представляет собой амплитуду в начальный момент времени. Начальное смещение x0 зависит, кроме a0, также от начальной фазы α: x0 = a0 ⋅ cosα.
Скорость затухания колебаний определяется коэффициентами затухания 
. Найдём время τ, за которое амплитуда уменьшается в е раз. По определению 
, откуда 
. Следовательно, коэффициент затухания обратен по величине тому промежутку времени, за который амплитуда уменьшается в е раз.
Период затухающих колебаний равен
(4.1.66)
.
При незначительном сопротивлении среды 
период колебаний практически равен 
.
Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно
(4.1.67)
.
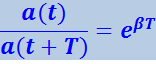Это отношение называют декрементом затухания, а его логарифм – логарифмическим декрементом затухания:
(4.1.68)
.
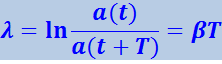Для характеристики колебательной системы обычно используется логарифмический декремент затухания λ. Выразив в соответствии с (4.1.68) β через λ и T, можно закон убывания амплитуды со временем записать в виде
.
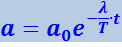За время τ, за которое амплитуда уменьшается в е раз, система успевает совершить 
колебаний. Из условия 
получается, что 
. Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз.
Для характеристики колебательной системы часто употребляется также величина
(4.1.69)
,
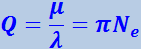называемая добротностью колебательной системы. Как видно из её определения, добротность пропорциональна числу колебаний 
, совершаемых системой за то время τ, за которое амплитуда уменьшается в е раз.
Из (4.1.14) следует, что полная энергия колеблющейся системы пропорциональна квадрату амплитуды. В соответствии с этим энергия системы при затухающих колебаниях убывает со временем по закону
(4.1.70)
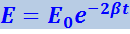
(E0 - значение энергии при t = 0).
Продифференцировав это выражение по t, получим скорость возрастания энергии системы:
.
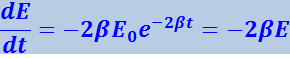Изменив знак на обратный, найдём скорость убывания энергии:
(4.1.71)
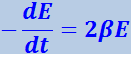
Если энергия мало изменяется за время, равное периоду колебаний, убыль энергии за период можно найти, умножив (4.1.71) наТ:
.
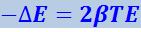Наконец, приняв во внимание формулы (4.1.68) и (4.1.69), получим:
(4.1.72)
,
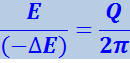из которого следует, что при слабом затухании колебаний добротность с точностью до множителя 2π равна отношению энергии, запасённой в системе в данный момент к убыли этой энергии за один период колебаний.
Из формулы (4.1.66) следует, что с ростом коэффициента затухания период увеличивается. При β = ω0 период колебаний обращается в бесконечность, т.е. движение перестаёт быть периодическим.
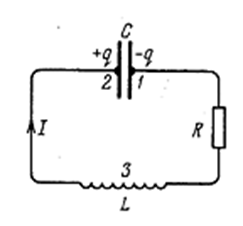
Теперь рассмотрим электрические затухающие колебания в колебательном контуре. Всякий реальный контур обладает активным сопротивлением R. Энергия, запасённая в контуре, постепенно расходуется в этом сопротивлении на нагревание, вследствие чего свободные колебания затухают. Запишем закон Ома для цепи 1-3-2, изображённой на рис. 4.1.17:
(4.1.73)
.
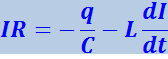Рис. 4.1.17 |
Разделив это уравнение на L и заменив I через 
, а 
через 
, получим:
(4.1.74)
.
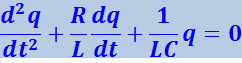Приняв во внимание, что величина обратная LC, равна квадрату собственной частоты контура ω0, и введя обозначение
(4.1.75)
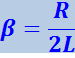
(β - коэффициент затухания), уравнению (4.1.74) можно придать вид
(4.1.76)
.
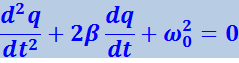Последнее уравнение совпадает с дифференциальным уравнением (4.1.63) затухающих механических колебаний.
При условии, что 
, решение уравнения (4.1.76) имеет вид
(1.77)
,
где 
. Подставив значение (4.1.38) для 
и (4.1.75) для β, найдём, что
(1.78)
.
Таким образом, частота затухающих колебаний ω меньше собственной частоты 
.
Разделив (4.1.77) на ёмкость С, получим напряжение на конденсаторе:
(1.79)
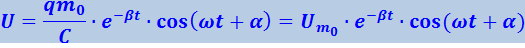
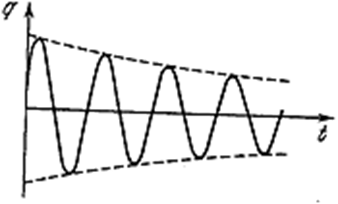
Чтобы найти силу тока, надо продифференцировать (4.1.77) по времени. График функции (4.1.77) изображён на рис. 4.1.18. Графики для напряжения и силы тока имеют аналогичный вид.
Рис. 4.1.18 |
Затухание электромагнитных колебаний, как и механических, характеризуются логарифмическим декрементом затухания:
(4.1.80)
.
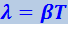Подставив в (4.1.80) (4.1.75) и заменив через 
, получим:
(4.1.81)
.
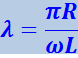Если затухание невелико 
, то можно положить в (4.1.81) 
. Тогда
(4.1.82)
.
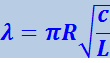Часто колебательный контур характеризуют его добротностью
(1.83)
.
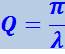Подставив в (4.1.83) (4.1.82) получим, что в случае слабого затухания добротность определяется соотношением:
(4.1.84)
.
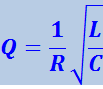В заключение отметим, что при 
, т.е. при 
, вместо колебаний происходит апериодический разряд конденсатора. Сопротивление, при котором колебательный процесс переходит апериодический, называется критическим. Значение критического сопротивления 
определяется условием 
, откуда
(4.1.85)
.
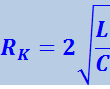к к к