‘»«» ј
4.1.6. Сложение взаимно перпендикулярных колебаний
Допустим, что материальная точка может совершать колебания как вдоль оси х, так и вдоль перпендикулярной к ней оси y. Если возбудить оба колебания, материальная точка будет двигаться по некоторой криволинейной траектории, форма которой зависит от разности фаз обоих колебаний.
Выберем начало отсчёта времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний запишутся следующим образом:
(4.1.50)
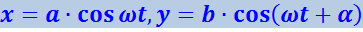 ,
,
где α - разность фаз обоих колебаний.
Выражения (4.1.50) представляют собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Чтобы получить уравнение траектории в обычной форме, надо исключить из уравнений (4.1.50) параметр t. Из первого уравнения следует, что
(4.1.51)
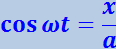 .
.
Следовательно,
(4.1.52)
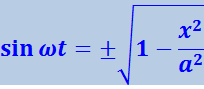 .
.
Теперь развернём косинус во втором из уравнений (4.1.50) по формуле для косинуса суммы, подставляя при этом вместо cosωt и sinωt их значения (4.1.51) и (4.1.52). В результате получим:
(4.1.53)
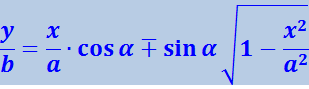 .
.
Уравнение (4.1.53) после преобразований можно привести к виду
(4.1.54)
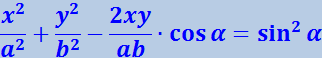 .
.
Последнее уравнение – уравнение эллипса, оси которого повёрнуты относительно координатных осей х и y. Ориентация эллипса и величина его полуосей довольно сложным образом зависят от амплитуд a и b и разности фаз α.
Определим форму траектории для некоторых частных случаев.
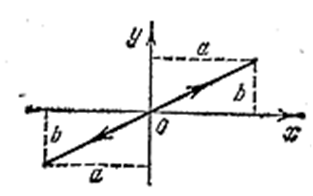
- Разность фаз α равна нулю. В этом случае уравнение (4.1.54) принимает вид
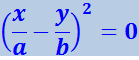 ,
,
откуда получается уравнение прямой
(4.1.55)
 .
.
Рис. 4.1.12 |
Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и амплитудой, равной ![]() (рис. 4.1.12).
(рис. 4.1.12).
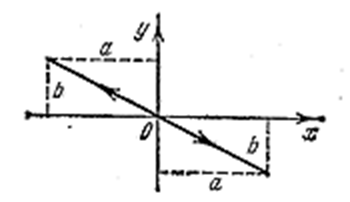
- Разность фаз α = ±π. Уравнение (4.1.54) имеет вид
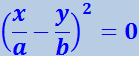 ,
,
откуда получается, что результирующее движение, представляет собой гармоническое колебание вдоль прямой (рис. 4.1.13):
(4.1.56)
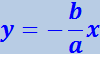 .
.
Рис. 4.1.13 |
- При
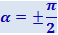 уравнение (4.1.54) переходит в
уравнение (4.1.54) переходит в
(4.1.57)
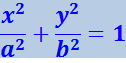 ,
,
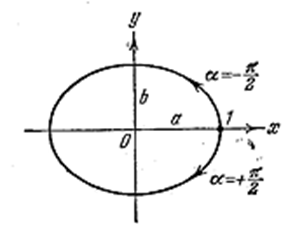
т.е. в уравнение эллипса, приведённого к координатным осям, причём полуоси эллипса равны соответствующим амплитудам колебаний (рис. 4.1.14).
Рис. 4.1.14 |
При равенстве амплитуд a и b эллипс вырождается в окружность.
Случаи ![]() и
и ![]() отличаются направлением движения по эллипсу или по окружности. Если
отличаются направлением движения по эллипсу или по окружности. Если ![]() , уравнения (4.1.50) можно записать следующим образом:
, уравнения (4.1.50) можно записать следующим образом:
(4.1.58)
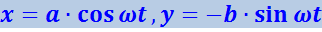 .
.
В момент t = 0 тело находится в точке 1 (рис. 4.1.14). В последующие моменты времени координата х уменьшается, а координата y становится отрицательной. Следовательно, движение совершается по часовой стрелке.
При ![]() уравнения колебаний имеют вид:
уравнения колебаний имеют вид:
(4.1.59)
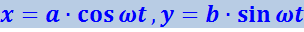 .
.
Отсюда можно заключить, что движение происходит против часовой стрелки.
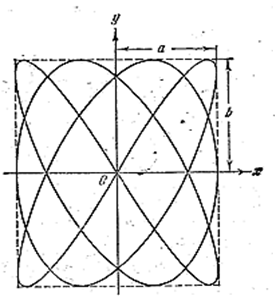
Если частоты взаимно перпендикулярных колебаний неодинаковы, то траектория результирующего движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу. На рис. 4.1.15 для примера показана кривая для отношения частот 3:4 и разности фаз π/2. Существует атлас фигур Лиссажу.
Рис. 4.1.15 |
к к к