ФИЗИКА
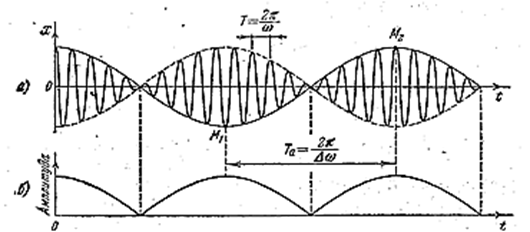
Особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. Результирующее движение в этом случае можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такое колебание называется биениями.
Обозначим частоту одного из колебаний ω, частоту второго колебания через ω + Δω. По условию Δω<< ω. Амплитуды обоих колебаний будем полагать одинаковыми и равными a. Допустим, что начальные фазы колебаний равны нулю. Тогда уравнения колебаний будут иметь следующий вид:
.
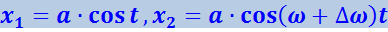Складывая эти выражения, получим:
(4.1.48)
(во втором множителе пренебрегаем членом 
по сравнению с ω). График функции (4.1.48) изображён на рис. 4.1.11а. График построен для 
.
Заключённый в скобки множитель в (4.1.48) изменяется гораздо медленнее, чем второй множитель. Это даёт нам основание рассматривать колебание (4.1.48) как гармоническое колебание частоты ω, амплитуда которого изменяется по некоторому периодическому закону. Выражением этого закона не может быть множитель, стоящий в скобках, так как он изменяется в пределах от -2a до +2a, в то время как амплитуда по определению – положительная величина. График амплитуды показан на рис. 1.11б. Аналитическое выражение амплитуды имеет вид:
(4.1.49)
.
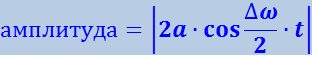Рис. 4.1.11 |
Функция (4.1.49) – периодическая функция с частотой, вдвое превышающей частоту выражения, стоящего пол знаком модуля. Таким образом, частота пульсаций амплитуды – её называют частотой биений – равна разности частот складываемых колебаний.
Множитель 
не только определяет амплитуду, но и влияет на фазу колебания. Это проявляется, например, в том, что отклонения, соответствующие соседним максимумам амплитуды, имеют противоположные знаки (точки M1 и М2 на рис. 4.1.11а).
к к к