ФИЗИКА
4.1.4. Сложение гармонических колебаний одинакового направления равных частот
Сложение нескольких колебаний одинакового направления значительно облегчается и становится наглядным, если изображать колебания графически в виде векторов на плоскости. Полученная таким способом схема называется векторной диаграммой.
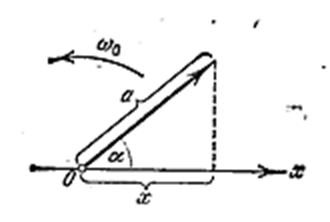
Возьмём ось, которую обозначим буквой х (рис. 4.1.9). Из точки О, взятой на оси, отложим вектор длины a, образующий с осью угол α. Если привести этот вектор во вращение с угловой скоростью ω0, то проекция конца вектора будет перемещаться по оси х в пределах от -a до +a, причём координата этой проекции будет изменяться со временем по закону
 .
.
Следовательно, проекция конца вектора на ось будет совершать гармоническое колебание с амплитудой, равной длине вектора, круговой частотой, равной угловой скорости вращения вектора, и начальной фазой, равной углу, образуемому вектором с осью в начальный момент времени.
Рис. 4.1.9 |
Из сказанного следует, что гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колебания, а направление вектора образует с осью х угол, равный начальной фазе колебания.
Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты. Смещение х колеблющегося тела будет суммой смещений x1 и x2, которые запишутся следующим образом:
(4.1.45)
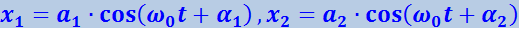
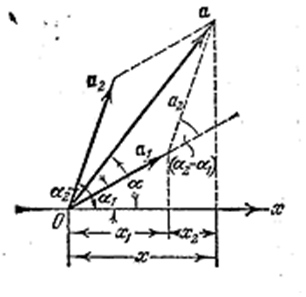
Представим оба колебания с помощью векторов a1 и a2 (рис. 4.1.10). Построим по правилам сложения векторов результирующий вектор А. Легко видеть, что проекция этого вектора на ось х равна сумме проекций слагаемых векторов:
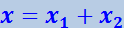 .
.
Следовательно, вектор a представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью ω0, как и векторы a1 и a2, так что результирующее движение будет гармоническим колебанием с частотой ω0, амплитудой a и начальной фазой α. Из построения видно, что
(4.1.46)
![]() ,
,
(4.1.47)
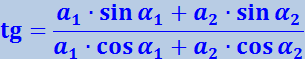 .
.
Рис. 4.1.10 |
Итак, представление гармонических колебаний посредством векторов даёт возможность свести сложение нескольких колебаний к операции сложения векторов. Этот приём бывает особенно полезен, например, в оптике или электротехнике.
Проанализируем выражение (4.1.46) для амплитуды. Если разность фаз обоих колебаний α2 - α1 равна нулю, амплитуда результирующего колебания равна a = a1 + a2. Если разность фаз α2 - α1 равна +π или -π, т.е. оба колебания находятся в противофазе, то амплитуда результирующего колебания равна |a1 - a2|.
Если частоты колебаний x1 и x2 неодинаковы, векторы a1 и a2 будут вращаться с различной скоростью. В этом случае результирующий вектор А пульсирует по величине и вращается с непостоянной скоростью. Следовательно, результирующим движением будет в этом случае не гармоническое колебание, а некоторый сложный колебательный процесс.
к к к